1.2 Abstractions

To help manage complex problems and complex data types, computer scientists typically work with abstractions. An abstraction is a mechanism for separating the properties of an object and restricting the focus to those relevant in the current context. The user of the abstraction does not have to understand all of the details in order to utilize the object, but only those relevant to the current task or problem.

Two common types of abstractions encountered in computer science are procedural, or functional, abstraction and data abstraction. Procedural abstraction is the use of a function or method knowing what it does but ignoring how it's accomplished. Consider the mathematical square root function which you have probably used at some point. You know the function will compute the square root of a given number, but do you know how the square root is computed? Does it matter if you know how it is computed, or is simply knowing how to correctly use the function sufficient?

Data abstraction is the separation of the properties of a data type (its values and operations) from the implementation of that data type. You have used strings in Python many times. But do you know how they are implemented? That is, do you know how the data is structured internally or how the various operations are implemented?

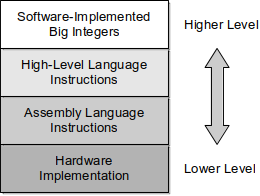
Figure 1.2.1: Levels of abstraction used with integer arithmetic.

Typically, abstractions of complex problems occur in layers, with each higher layer adding more abstraction than the previous. Consider the problem of representing integer values on computers and performing arithmetic operations on those values. Figure 1.2.1 illustrates the common levels of abstractions used with integer arithmetic. At the lowest level is the hardware with little to no abstraction since it includes binary representations of the values and logic circuits for performing the arithmetic. Hardware designers would deal with integer arithmetic at this level and be concerned with its correct implementation.

A higher level of abstraction for integer values and arithmetic is provided through assembly language, which involves working with binary values and individual instructions corresponding to the underlying hardware. Compiler writers and assembly language programmers would work with integer arithmetic at this level and must ensure the proper selection of assembly language instructions to compute a given mathematical expression. For example, suppose we wish to compute

$$x=a+b-5$$

At the assembly language level, this expression must be split into multiple instructions for loading the values from memory, storing them into registers, and then performing each arithmetic operation separately, as shown in the following pseudocode:

    loadFromMem( R1, 'a' )
    loadFromMem( R2, 'b' )
    add R0, R1, R2
    sub R0, R0, 5
    storeToMem( R0, 'x' )

To avoid this level of complexity, high-level programming languages add another layer of abstraction above the assembly language level. This abstraction is provided through a primitive data type for storing integer values and a set of well-defined operations that can be performed on those values. By providing this level of abstraction, programmers can work with variables storing decimal values and specify mathematical expressions in a more familiar notation

    x = a + b - 5

than is possible with assembly language instructions. Thus, a programmer does not need to know the assembly language instructions required to evaluate a mathematical expression or understand the hardware implementation in order to use integer arithmetic in a computer program.

One problem with the integer arithmetic provided by most high-level languages and in computer hardware is that it works with values of a limited size. On 32-bit architecture computers, for example, signed integer values are limited to the range $2^{31}\dots (2^{31}-1)$. What if we need larger values? In this case, we can provide long or "big integers" implemented in software to allow values of unlimited size. This would involve storing the individual digits and implementing functions or methods for performing the various arithmetic operations. The implementation of the operations would use the primitive data types and instructions provided by the high-level language. Software libraries that provide big integer implementations are available for most common programming languages. Python, however, actually provides software-implemented big integers as part of the language itself.