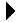7.6 Revisiting The Bag ADT

To illustrate the use of the linked list structure, we implement a new version of the Bag ADT, which we originally defined in Section 2.1. As a review, the definition for the Bag ADT is provided below:

The Bag ADT

A bag is a container that stores a collection in which duplicate values are allowed. The items, each of which is individually stored, have no particular order but they must be comparable.

Bag()

Creates a bag that is initially empty.
length()

Returns the number of items stored in the bag. Accessed using the len function.
contains()

Determines if the given target item is stored in the bag and returns the appropriate Boolean value. Accessed using the in operator.
add(item)

Adds the given item to the bag.
remove(item)

Removes and returns an occurrence of item from the bag. An exception is raised if the element is not in the bag.
iterator()

Creates and returns an iterator that can be used to iterate over the collection of items.

A Linked List Implementation

Up to this point, we have mainly used the Python list to implement a variety of abstract data types. The singly linked list can also be used to implement a wide range of abstract data types. The choice of the underlying data structure depends heavily on the efficiency of the various operations of the abstract data type being implemented. The ultimate goal is to provide the most efficient implementation possible. Thus, the Python list or vector is not always the best choice for implementing some abstract data types.

The Bag ADT provides a simple example of how to implement an abstract data type using a singly linked list. The items in the bag will be stored in the individual nodes of the list, one item per node. To implement a new version of the Bag ADT, we must define a new class with all of the same methods as the original version. This version will be stored in a module named llistbag.py.

As a reminder, a linked list is not itself an abstract data type. Instead, system components (references and objects) are used as building blocks to construct the dynamic linear structure. Each time you implement an abstract data type using a linked list, you must include some of the same code each time.

Storage Class

We begin our discussion of the linked list implementation of the Bag ADT with the definition of a storage class used to represent the individual nodes. The node storage class will have the same structure as that used in the previous sections, but we use the name BagListNode to indicate that it is for use in implementing the Bag ADT. The storage class must be defined within the same module, but it is not intended for use outside the Bag class. Thus, we will include it at the bottom of the module. The definition of the storage class is provided below:

class BagListNode :

  def __init__(self, data) :

    self.data = data

    self.next = None

Constructor

We begin the implementation with the constructor. Each instance of the class will need two attributes: the head reference and the number of elements in the bag.

class Bag :

  def __init__(self) :  

    self._head = None

    self._size = 0

The _head attribute will store a reference to the head node of the linked list in order to provide access to the nodes. The reference is initialized to None to represent an empty bag. The _size field is used to keep track of the number of items stored in the bag, which will be needed by the __len__ method. Technically, this field is not needed. But it does prevent us from having to traverse the list to count the number of nodes each time the length is needed. A sample instance of the new Bag class is illustrated in Figure 7.6.1.

Figure 7.6.1: Sample instance of the Bag class.

NOTE
	You may have noticed that we only define a head reference as a data field in the object. Temporary references such as the `curNode` reference used to traverse the list are not defined as attributes, but instead as local variables within the individual methods as needed.

Bag Size

The length operation returns the number of items contained in the bag. This method simply returns the value of the _size attribute, which is used to keep track of this value.

  def __len__(self) :

    return self._size

Question 7.6.1

What is the time-complexity for the length operation?

Select the correct answer below by clicking on the appropriate box.

O(1)
O(log n)
O(n)
O(n²)

Returning the value of an instance variable is a constant time operation.

Question 7.6.2

Had we not included the _size instance variable in our implementation, we could not simply return the value of a variable. What would be the time-complexity for the __len__ method in this case?

Select the correct answer below by clicking on the appropriate box.

O(1)
O(log n)
O(n)
O(n²)

The number of items in the bag would have to be determined by counting the number of nodes in the linked list. This could only be done by traversing the list and counting the number of iterations required for the complete traversal.

Contains Method

The __contains__ method is a simple search of the linked list as described earlier in the chapter. The implementation is identical to the searchList function from Section List. The only difference is that searchList is a function to which you must pass the head reference of the linked list to be searched. Here, we are implementing a method and the head reference is an instance variable that can be accessed directly from each method. The implementation of the search operation is provided below:

  def __contains__(self, target) :

    curNode = self._head

    while curNode and curNode.item != target :

      curNode = curNode.next    

    return curNode is not None

Question 7.6.3

Is the linked list search more efficient than the linear search performed on a Python list?

Select the correct answer below by clicking on the appropriate box.

Both require linear time.

Adding an Item

To add an item to the bag, we will need to store the item in a node and link the node into the linked list. Since a bag has no specific ordering, we can prepend the new node onto the linked list using the same code from Section 7.4. The only difference is that we must also increment the item counter as new items are added. Here is the code for the add method:

  def add(self, item) :

    newNode = BagListNode(item) 

    newNode.next = self._head

    self._head = newNode

    self._size += 1

Question 7.6.4

What is the time-complexity for the add operation?

Select the correct answer below by clicking on the appropriate box.

O(1)
O(log n)
O(n)
O(n²)

We saw earlier that prepending a node onto a linked list can be done in constant time. The implementation of this method is basically the same other than incrementing the counter, which is itself a constant time operation.

Removing an Item

The remove method implements the removal operation as presented in Section 7.5, but with several modifications.

  def remove(self, item):

    predNode = None

    curNode = self._head

    while curNode and curNode.item != item :  

      predNode = curNode

      curNode = curNode.next                                

     # The item has to be in the bag to remove it.

    assert curNode is not None, "The item must be in the bag."

     # Unlink the node and return the item.

    self._size -= 1      

    if curNode is self._head :                                  

      self._head = curNode.next                                 

    else :           

      predNode.next = curNode.next

    return curNode.item

The if statement that checked the status of the curNode reference variable has been replaced with an assert statement. This is necessary since the remove operation of the bag has a precondition that the item must be in the bag in order to be removed. If we make it pass the assertion, the item counter is decremented to reflect one less item in the bag, the node containing the item is unlinked from the linked list, and the item is returned as required by the ADT definition.

Question 7.6.5

What would happen if we omit the statement <code> self._size = self._size - 1 </code> which decrements the bag size counter?

The length operation would not provide the correct value when used after items have been removed from the bag. The value returned would not reflect the correct number of items in the bag.

The New Implementation

The new implementation of the Bag ADT using a singly linked list is shown in the source listing below:

Program Listing

Program: llistbag.py

# Implements the Bag ADT using a singly linked list.
class Bag :
# Constructs an empty bag.
def __init__(self) :
self._head = None
self._size = 0
# Returns the number of items in the bag.
def __len__(self) :
return self._size
# Determines if an item is contained in the bag.
def __contains__(self, target) :
curNode = self._head
while curNode and curNode.item != target :
curNode = curNode.next
return curNode is not None
# Adds a new item to the bag.
def add(self, item) :
newNode = _BagListNode(item)
newNode.next = self._head
self._head = newNode
self._size += 1
# Removes an instance of the item from the bag.
def remove(self, item):
predNode = None
curNode = self._head
while curNode and curNode.item != item :
predNode = curNode
curNode = curNode.next
# The item has to be in the bag to remove it.
assert curNode is not None, "The item must be in the bag."
# Unlink the node and return the item.
self._size -= 1
if curNode is self._head :
self._head = curNode.next
else :
predNode.next = curNode.next
return curNode.item
# Defines a storage class for creating list nodes.
class BagListNode :
def __init__(self, item) :
self.item = item
self.next = None

Comparing Implementations

The Python list and the linked list can both be used to manage the elements stored in a bag. Both implementations provide the same time-complexities for the various operations with the exception of the add method. When adding an item to a bag implemented using a Python list, the item is appended to the list, which requires $O (n)$ time in the worst case since the underlying array may have to be expanded. In the linked list version of the Bag ADT, a new bag item is stored in a new node that is prepended to the linked structure, which only requires constant time. Table 7.6.1 shows the time-complexities for two implementations of the Bag ADT.

	Python List	Linked List
`b = Bag()`	$O (1)$	$O (1)$
`n = len(b)`	$O (1)$	$O (1)$
`x in b`	$O (n)$	$O (n)$
`b.add(x)`	$O (n)$	$O (1)$
`b.remove(x)`	$O (n)$	$O (n)$
traversal	$O (n)$	$O (n)$

Table 7.6.1: Comparing the Bag ADT implemented using a Python list and a linked list.

In general, the choice between a linked list or a Python list depends on the application as both have advantages and disadvantages. The linked list is typically a better choice for those applications involving large amounts of dynamic data, data that changes quite often. If there will be a large number of insertions and/or deletions, the linked structure provides a fast implementation since large amounts of data do not have to be shifted as is required by the Python list. This is especially true when prepending items. On the other hand, the Python list is a better choice in those applications where individual elements must be accessed by position. This can be simulated with a linked list, but it requires a traversal of the list, resulting in a linear operation whereas the Python list only requires constant time.

Question 7.6.6

Would the linked list be an ideal structure for implementing the Polygon ADT that was presented earlier this term?

Since the Polygon is an indexed sequence in which the elements need to be accessed by position, the linked list would not be a good structure for implementing the Polygon ADT. The Python list was the best choice for the implementation.

7.5 Removing Nodes from a Linked List

Chapter 7. Linked Structures

7.7 Linked List Iterators