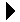3.5 Designing an Expandable Container

Like all abstract data types, the vector ADT has to be implemented before it can be used. Since the vector is an indexed ordered sequence whose elements are accessible by position, the vector is typically implemented using a one-dimensional array. By definition, a vector can contain any number of items and never becomes full. But as you learned earlier, the array has a fixed size. Once created the size can not be changed. To use the array in the implementation of a vector, we must provide a way for the abstract view of the vector to grow and shrink as new elements are added or removed.

To use an array to implement an expandable container, we can start with an initial small array and keep replacing it with ever larger arrays as new elements are added. For efficiency, which you will learn about later in Chapter 5, we do not want to replace the array each time a new element is added. Instead, when an array is created for the vector, it is created to be larger than what is actually needed.

Creating the Initial Array

Suppose we create a vector (or Python list) containing several values:

which would produce the follwoing abstract view of the vector

To provide a physical implementation, we can create an array to store the elements of the vector that is initially larger than needed.

The elements of the vector are stored at the front of the array and comprise a subarray in which only a contiguous subset of array elements are initially used. As you can see, the subarray represents the abstract view of the vector. The elements of the array with null references are the remaining elements of the array into which the vector can expand. Thus, we leave capacity for future expansion of the vector without having to create a new larger array every time a new element is added.

Figure 3.5.1 illustrates both the abstract and physical views of our sample list. In the physical view, the elements of the array used to store the actual contents of the list are shown inside the dashed yellow box. The elements outside the dashed box provide the extra capacity for future expansion of the vector. This notation will be used in this and the next section to illustrate the contents of the vector and the underlying array used to implement it.

Figure 3.5.1: The abstract and physical views of a list implemented using an array.

When working with a subarray, we must keep track of the number of elements that comprise the subarray. This value represents the length of the vector. The size or capacity of the array used to implement the vector must also be maintained in order to know when the array becomes full through inserting and appending new elements to the vector.

Replacing the Array

What happens when a new item is appended to the end of a vector (or Python list)

If there is room in the array, the item is stored in the next available slot of the array and the length field is incremented by one. The result of appending 50 to values is shown below

What happens when the array becomes full and there are no free elements in which to add a new list item? For example, consider the following list operations:

After the second statement is executed, the array becomes full and there is no available space to add more values as illustrated below

By definition, a vector (i.e, the Python list) can contain any number of items and never becomes full. Thus, when the third statement is executed, the array will have to be expanded to make room for value 6. From the discussion earlier in the chapter, we know an array cannot change size once it has been created. To allow for the expansion of the list, the following steps have to be performed:

1. A new array is created with additional capacity. Typically, the new array is double the size of the original.
   

   
   

2. The items from the original array are copied to the new larger array, element by element.
   

   
   

3. The new larger array is set as the data structure for the vector and the original smaller array is destroyed.
   

   
   

After the array has been expanded, the value can be appended to the end of the vector.

In Python, the amount by which the size of the array is increased is proportional to the current array size. For illustration purposes, we assume an expansion creates a new array that is double the size of the original.