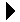8.5 Unbounded Priority Queue

On this page...

Python List Implementation
Linked List Implementation

There are a number of ways to implement an unbounded Priority Queue ADT. The most basic is to use a vector or linked list as was done with the Queue ADT. To implement the priority queue, we must consider several facts related to the definition of the ADT:

A priority must be associated with each item in the queue, possibly requiring the value to be stored along with the item.
The next item to be dequeued from the priority queue is the item with the highest priority.
If multiple items have the same priority, those items must be dequeued in the order they were originally enqueued.

Python List Implementation

We used a Python list to implement the basic queue earlier in the chapter. In that implementation, the queue items were organized within the list from front to back with new items appended directly to the end and existing items removed from the front. That simple organization worked well with the basic queue. When implementing the priority queue, however, the items cannot simply be added directly to the list, but instead we must have a way to associate a priority with each item. This can be accomplished with a simple storage class containing two fields: one for the priority and one for the queue item. For example:

class PriorityQEntry :

  def __init__(self, item, priority) :

    self.item = item

    self.priority = priority

With the use of a storage class for maintaining the associated priorities, the next question is how should the entries be organized within the vector? Remember, the actual implementation or physical organization of the data items do not have to match the abstract view of the ADT. We can organize the data items any way we like so long as the operations are implemented to correctly provide the abstract view. Thus, we can consider two approaches, both of which satisfy the requirements of the priority queue:

Keep the items sorted within the vector based on their priority.
When a new item is enqueued, find its proper position within the list based on its priority and insert an instance of the storage class at that point. If we order the items in the vector from lowest priority at the front to highest at the end, then the dequeue operation simply requires the removal of the last item in the list. To maintain the proper ordering of items with equal priority, the enqueue operation must ensure newer items are inserted closer to the front of the list than the other items with the same priority.
Append new items to the end of the vector.

When a new item is enqueued, simply append a new instance of the storage class (containing the item and its priority) to the end of the list. When an item is dequeued, search the vector for the item with the lowest priority and remove it from the list. If more than one item has the same priority, the first one encountered during the search will be the first to be dequeued.

In this section, we provide an implementation using the latter approach in which new items are appended to the end of the vector. The implementation of the alternative approach is left as an exercise.

Most of the operations of the priority queue can be implemented in the same fashion as with the basic queue. Only the enqueue and dequeue methods are different. When a new item is enqueued, a new storage object is created to store the item and its priority. The storage object is then appended to the end of the vector:

def enqueue(self, item, priority) :

  entry = PriorityQEntry(item, priority) 

  self._qList.append(entry)

Thus, in the physical representation the items are stored in the order in which they are enqueued, not in the order in which they will be dequeued. This can be seen in Figure 8.5.1, which illustrates an instance of the class for the priority queue from Figure 8.4.1.

Figure 8.5.1: An instance of the priority queue implemented using a Python list.

To dequeue an item, we can not simply remove the first item in the vector since the items are not stored in order by priority. Instead, we have to search through the vector to find the item with the highest priority. Once found, the item can be removed from the vector and returned. The dequeue method is shown below:

def dequeue(self) :

  assert not self.isEmpty(), "Cannot dequeue from an empty queue."    

  highest = self._qList[i].priority 

  for i in range(self.len()) :

    if self._qList[i].priority < highest :

      highest = self._qList[i].priority

  entry = self._qList.pop(highest)

  return entry.item   # only the item part is returned.

A complete implementation of the priority queue in which new items are appended to the end of the vector is provided below.

Program Listing

Program: priorityq.py

# Implementation of the unbounded Priority Queue ADT using a Python list
# with new items appended to the end.
class PriorityQueue :
# Create an empty unbounded priority queue.
def __init__(self) :
self._qList = list()
# Returns True if the queue is empty.
def isEmpty(self) :
return len(self) == 0
# Returns the number of items in the queue.
def __len__(self) :
return len( self._qList )
# Adds the given item to the queue.
def enqueue(self, item, priority) :
# Create a new instance of the storage class and append it to the list.
entry = PriorityQEntry(item, priority)
self._qList.append(entry)
# Removes and returns the item with the highest priority in the queue.
def dequeue(self) :
assert not self.isEmpty(), "Cannot dequeue from an empty queue."
# Find the entry with the highest priority.
highest = self._qList[i].priority
for i in range(self.len()) :
# See if the ith entry contains a higher priority (smaller integer).
if self._qList[i].priority < highest :
highest = self._qList[i].priority
# Remove the entry with the highest priority and return the item.
entry = self._qList.pop(highest)
return entry.item
# Private storage class for associating queue items with their priority.
class PriorityQEntry :
def __init__(self, item, prioity) :
self.item = item
self.priority = priority

To evaluate the efficiency, we consider the implementation of each operation. Testing for an empty queue and determining the size can be done in $O (1)$ time. The enqueue operation requires linear time in the worst case since the underlying array may have to be reallocated, but it has a $O (1)$ amortized cost. The dequeue operation is also $O (n)$ since we must search through the entire list in the worst case to find the entry with the highest priority.

Linked List Implementation

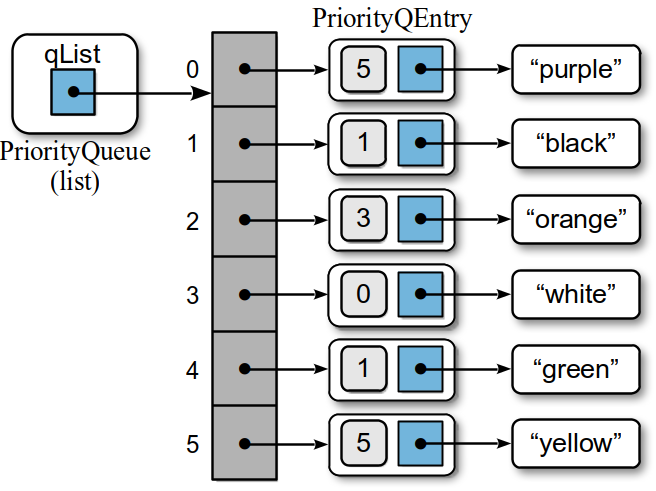
A singly linked list structure with both head and tail references can also be used to implement the priority queue as illustrated in Figure 8.5.2. The QueueNode class used in the implementation of the Queue ADT using a linked list has to be modified to include the priority value. After that, the linked list can be used in a similar fashion as the Python list. When an item is enqueued, the new node is appended to the end of the linked list and when a dequeue operation is performed, the linked list is searched to find the entry with the highest priority. We leave the actual design and implementation as an exercise but examine the time-complexity of this approach.

Figure 8.5.2: Physical representation of the sample priority queue using a linked list.

As with the Python list implementation of the priority queue, testing for an empty queue and determining the size can be done in $O (1)$ time. The enqueue operation can also be done in constant time since we need only append a new node to the end of the list. The dequeue operation, however, requires $O (n)$ time since the entire list must be searched in the worst case to find the entry with the highest priority. Once that entry is located, the node can be removed from the list in constant time.

8.4 Priority Queues

Chapter 8. Queues

8.6 Bounded Priority Queue