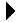8.3 Circular Array Implementation

On this page...

Data Organization
Queue Implementation
Run Time Analysis

The Python list-based implementation of the Queue ADT is easy to implement, but it requires linear time for the enqueue and dequeue operations. We can improve these times using an array structure and treating it as a circular array. A circular array is simply an array viewed as a circle instead of a line. An example is illustrated in Figure 8.3.1.

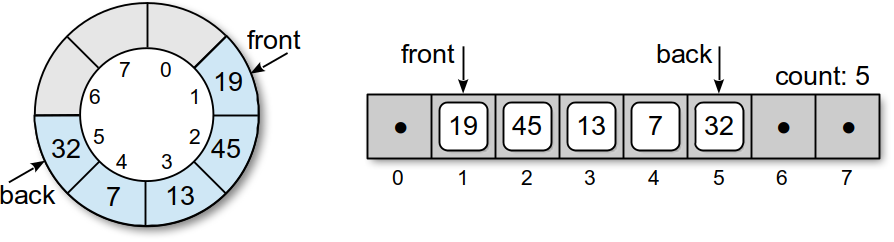
Figure 8.3.1: The abstract view of a circular array (left) and the physical view (right).

A circular array allows us to add new items to a queue and remove existing ones without having to shift items in the process. Unfortunately, this approach introduces the concept of a maximum-capacity queue that can become full. A circular array queue implementation is typically used with applications that only require small-capacity queues and allows for the specification of a maximum size.

Data Organization

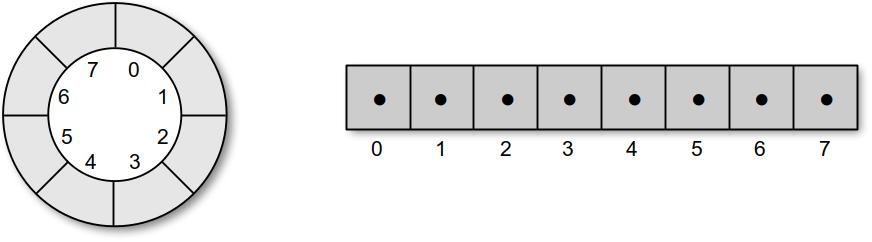
To implement a queue as a circular array, we must maintain a count field and two markers. The count field is necessary to keep track of how many items are currently in the queue since only a portion of the array may actually contain queue items. The markers indicate the array elements containing the first and last items in the queue. Consider the following circular array:

which illustrates the implementation of the queue from Figure 8.1.1. The figure shows the corresponding abstract and physical views of the circular array.

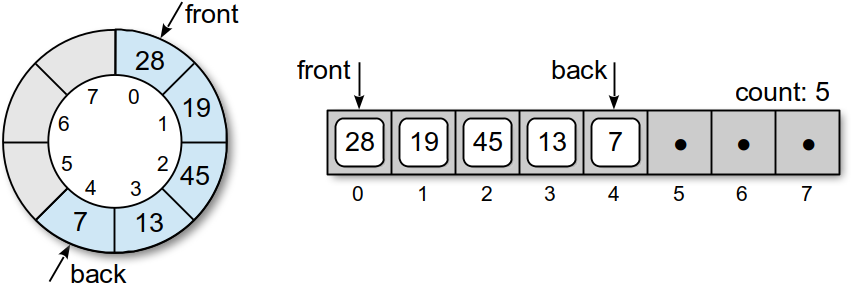
New items are added to the queue by inserting them in the position immediately following the back marker. The marker is then advanced one position and the counter is incremented to reflect the addition of the new item. For example, suppose we enqueue value 32 into the sample queue. The back marker is advanced to position 5 and value 32 is inserted:

To dequeue an item, the value in the element marked by front will be returned and the marker is advanced one position:

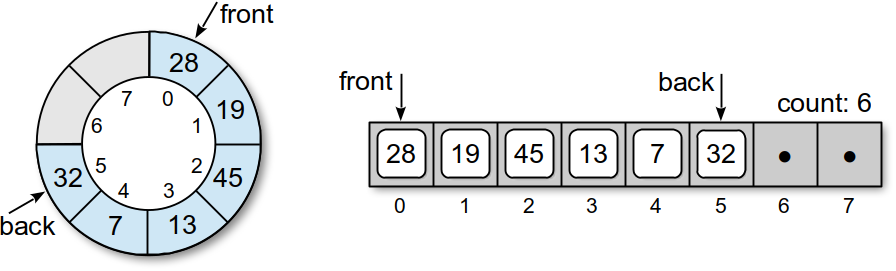
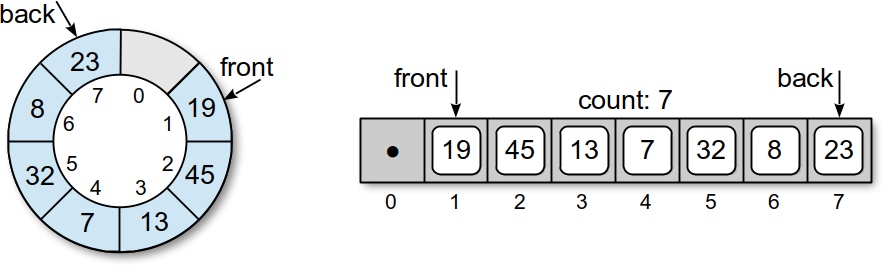
Notice the remaining items in the queue are not shifted. Instead, only the front marker is moved. Now, suppose we add values 8 and 23 to the queue. These values are added in the positions following the back marker:

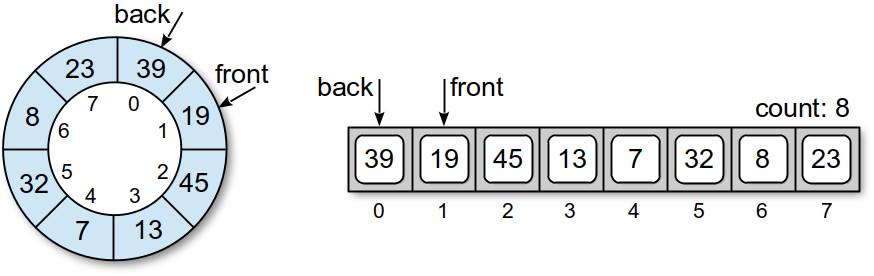
The queue now contains seven items in elements $[1 \dots 7]$ with one empty slot. What happens if value 39 is added? Since we are using a circular array, the same procedure is used and the new item will be inserted into the position immediately following the back marker. In this case, that position will be element 0. Thus, the queue wraps around the circular array as items are added and removed, which eliminates the need to shift items. The resulting queue is shown here:

This also represents a full queue since all slots in the array are filled. No additional items can be added until existing items have been removed. This is a change from the original definition of the Queue ADT and requires an additional operation to test for a full queue.

Queue Implementation

Given the description of a circular array and its use in implementing a queue, we turn our attention to the implementation details. The constructor creates an object containing four data fields, including the counter to keep track of the number of items in the queue, the two markers, and the array itself:

def __init__(self, maxSize) :

  self._count = 0

  self._front = 0

  self._back = maxSize - 1

  self._qArray = Array(maxSize)

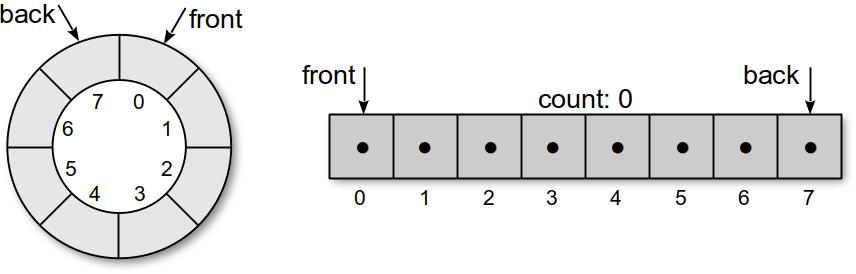
Figure 8.3.2 illustrates the circular array when first created by the constructor. The array is created with maxSize elements as specified by the argument to the constructor. The two markers are initialized so the first item will be stored in element $0$ . This is achieved by setting _front to $0$ and _back to the index of the last element in the array. When the first item is added, _back will wrap around to element $0$ and the new value will be stored in that position.

Figure 8.3.2: The circular array when the queue is first created by the constructor.

Figure 8.3.3 illustrates an instance of the class for the queue from Figure 8.1.3. The __len__ and isEmpty methods use the value of _count to return the appropriate result.

def isEmpty(self) :

  return self._count == 0

def __len__(self) :

  return self._count

Figure 8.3.3: A Queue object implemented as a circular array.

As indicated earlier, implementing the Queue ADT as a circular array creates the special case of a queue with a maximum capacity, which can result in a full queue. For this implementation of the queue, we must add the isFull method, which can be used to test if the queue is full. Again, the _count field is used to determine when the queue becomes full.

def isFull(self) :

  return self._count == len(self._qArray)

To enqueue an item, we must first test the precondition and verify the queue is not full. If the condition is met, the new item can be inserted into the position immediately following the _back and then incrementing the _back marker by 1. But remember, we are using a circular array and once the marker reaches the last element of the actual linear array, it must wrap around to the first element. This could be done using a condition statement to test if _back is referencing the last element and adjusting it appropriately, as shown here:

  self._back += 1

  if self._back == len(self._qArray) :

    self._back = 0

A simpler approach, however, is to use the modulus operator as part of the increment step. This reduces the need for the conditional and automatically wraps the marker to the beginning of the array as follows:

  self._back = (self._back + 1) % len(self._qArray)

The complete implementation of the enqueue operation is shown below:

def enqueue(self, item) :           

  assert not self.isFull(), "Cannot enqueue to a full queue."

  maxSize = len(self._qArray)

  self._back = (self._back + 1) % maxSize 

  self._qArray[self._back] = item

  self._count += 1

The dequeue operation is implemented in a similar fashion as enqueue:

def dequeue(self) :                 

  assert not self.isEmpty(), "Cannot dequeue from an empty queue."

  item = self._qArray[ self._front ]

  maxSize = len(self._qArray)

  self._front = (self._front + 1) % maxSize

  self._count -= 1

  return item

The item to be removed is taken from the position marked by _front and saved in the variable item. The marker is then advanced using the modulus operator as was done when enqueuing a new item. The counter is decremented and the saved item is returned. The complete implementation of the Queue ADT using a circular array is provided in the listing below:

Program Listing

Program: arrayqueue.py

# Implementation of the Queue ADT using a circular array.
from ezarrays import Array
class Queue :
# Creates an empty queue.
def __init__(self, maxSize) :
self._count = 0
self._front = 0
self._back = maxSize - 1
self._qArray = Array(maxSize)
# Returns True if the queue is empty.
def isEmpty(self) :
return self._count == 0
# Returns True if the queue is full.
def isFull(self) :
return self._count == len(self._qArray)
# Returns the number of items in the queue.
def __len__(self) :
return self._count
# Adds the given item to the queue.
def enqueue(self, item) :
assert not self.isFull(), "Cannot enqueue to a full queue."
maxSize = len(self._qArray)
self._back = (self._back + 1) % maxSize
self._qArray[self._back] = item
self._count += 1
# Removes and returns the first item in the queue.
def dequeue(self) :
assert not self.isEmpty(), "Cannot dequeue from an empty queue."
item = self._qArray[ self._front ]
maxSize = len(self._qArray)
self._front = (self._front + 1) % maxSize
self._count -= 1
return item

Run Time Analysis

The circular array implementation provides a more efficient solution than the Python list. The operations all have a worst case time-complexity of $O (1)$ since the array items never have to be shifted. But the circular array does introduce the drawback of working with a maximum-capacity queue. Even with this limitation, it is well suited for some applications.

8.2 Queue Implementation

Chapter 8. Queues

8.4 Priority Queues