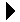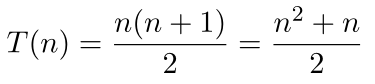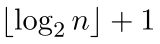5.3 Evaluating Python Code

As indicated earlier, when evaluating the time complexity of an algorithm or code segment, we assume that basic operations only require constant time. But what exactly is a basic operation? The basic operations include statements and function calls whose execution time does not depend on the specific values of the data that is used or manipulated by the given instruction. For example, the assignment statement

is a basic instruction since the time required to assign a reference to the given variable is independent of the value or type of object specified on the righthand side of the = sign. The evaluation of arithmetic and logical expressions

are basic instructions, again since they require the same number of steps to perform the given operations regardless of the values of their operands. The subscript operator, when used with Python's sequence types (strings, tuples, and lists) is also a basic instruction.

Linear Time Examples

Now, consider the following assignment statement:

An assignment statement only requires constant time, but that is the time required to perform the actual assignment and does not include the time required to execute any function calls used on the righthand side of the assignment statement.

To determine the run time of the previous statement, we must know the cost of the function call ex1(n). The time required by a function call is the time it takes to execute the given function. For example, consider the ex function, which computes the sum of the integer values in the range [$\mathit{\text{0 … n}}$):

The time required to execute a loop depends on the number of iterations performed and the time needed to execute the loop body during each iteration. In this case, the loop will be executed $\mathit{\text{n}}$ times and the loop body only requires constant time since it contains a single basic instruction. Note that the underlying mechanism of the for loop and the range function are both $\text{O}\left(1\right)$. We can compute the time required by the loop as $\mathit{\text{T(n) = n * 1}}$ for a result of $\text{O}\left(n\right)$.

NOTE

Efficiency of String Operations Most of the string operations have a time-complexity that is proportional to the length of the string. For most problems that do not involve string processing, string operations seldom have an impact on the run time of an algorithm. Thus, in the text, we assume the string operations, including the use of the print function, only require constant time, unless explicitly stated otherwise.

But what about the other statements in the function? The first line of the function and the return statement only require constant time. Remember, it's common to omit the steps that only require constant time and instead focus on the critical operations, those that contribute to the overall time. In most instances, this means we can limit our evaluation to repetition and selection statements and function and method calls since those have the greatest impact on the overall time of an algorithm. Since the loop is the only non-constant step, the function ex1 has a run time of $\text{O}\left(n\right)$. That means the statement y = ex1(n) from earlier requires linear time.

Next, consider the following function, which includes two for loops:

To evaluate the function, we have to determine the time required by each loop. The two loops each require $\text{O}\left(n\right)$ time as they are just like the loop in function ex1 earlier. If we combine the times, it yields $\mathit{\text{T(n) = n + n}}$ for a result of $\text{O}\left(n\right)$.

Quadratic Time Examples

When presented with nested loops, such as in the following,

the time required by the inner loop impacts the time of the outer loop. Both loops will be executed $\mathit{\text{n}}$, but since the inner loop is nested inside the outer loop, the total time required by the outer loop will be $\mathit{\text{T(n) = n × n}}$, resulting in a time of $\text{O}\left(n^2\right)$ for the ex3 function.

Not all nested loops result in a quadratic time. Consider the following function:

which has a time-complexity of $\text{O}\left(n\right)$. The function contains a nested loop, but the inner loop executes independent of the size variable $\mathit{\text{n}}$. Since the inner loop executes a constant number of times, it is a constant time operation. The outer loop executes $\mathit{\text{n}}$ times, resulting in a linear run time. The next example presents a special case of nested loops:

How many times does the inner loop execute? It depends on the current iteration of the outer loop. On the first iteration of the outer loop, the inner loop will execute one time; on the second iteration, it executes two times; on the third iteration, it executes three times, and so on until the last iteration when the inner loop will execute $\mathit{\text{n}}$ times. The time required to execute the outer loop will be the number of times the increment statement count += 1 is executed. Since the inner loop varies from $\mathit{\text{1}}$ to $\mathit{\text{n}}$ iterations by increments of $\mathit{\text{1}}$, the total number of times the increment statement will be executed is equal to the sum of the first $\mathit{\text{n}}$ positive integers:

which results in a quadratic time of $\text{O}\left(n^2\right)$.

Logarithmic Time Examples

The next example contains a single loop, but notice the change to the modification step. Instead of incrementing (or decrementing) by one, it cuts the loop variable in half each time through the loop.

To determine the run time of this function, we have to determine the number of loop iterations just like we did with the earlier examples. Since the loop variable is cut in half each time, this will be less than $\mathit{\text{n}}$. For example, if $\mathit{\text{n}}$ equals 16, variable i will contain the following five values during subsequent iterations (16, 8, 4, 2, 1).

Given a small number, it's easy to determine the number of loop iterations. But how do we compute the number of iterations for any given value of $\mathit{\text{n}}$? When the size of the input is reduced by half in each subsequent iteration, the number of iterations required to reach a size of one will be equal to

or the largest integer less than $lo{g}_{2}n$, plus 1. In our example of $\mathit{\text{n = 16}}$, there are $lo{g}_{2}16+16$, or four iterations. The logarithm to base $\mathit{\text{a}}$ of a number $\mathit{\text{n}}$, which is normally written as $y=lo{g}_{a}n$, is the power to which $\mathit{\text{a}}$ must be raised to equal $\mathit{\text{n}}$, or $\mathit{\text{n = a^y}}$. Thus, function ex6 requires $\text{O}\left(\text{log}n\right)$ time.

For values of $\mathit{\text{n}}$ that are not a power of 2, the number of iterations will be $\lceil {\log }_{2}n\rceil$ or the smallest integer greater than ${\log }_{2}n$. Since many problems in computer science that repeatedly reduce the input size do so by half, it's not uncommon to use $\log n$ to imply ${\log }_{2}n$ when specifying the run time of an algorithm.

Finally, consider the following definition of function ex7, which calls ex6 from within a loop. Since the loop is executed $\mathit{\text{n}}$ times and function ex6 requires logarithmic time, ex7 will have a run time of $\text{O}\left(n\text{log}n\right)$.

Different Cases

Some algorithms can have run times that are different orders of magnitude for different sets of inputs of the same size. These algorithms can be evaluated for their best, worst, and average cases. Algorithms that have different cases can typically be identified by the inclusion of an event-controlled loop or a conditional statement. Consider the following example, which traverses a list containing integer values to find the position of the first negative value. Note that for this problem, the input is the collection of $\mathit{\text{n}}$ values contained in the list.

At first glance, it appears the loop will execute $\mathit{\text{n}}$ times, where $\mathit{\text{n}}$ is the size of the list. But notice the return statement inside the loop, which can cause it to terminate early. If the list does not contain a negative value,

the return statement inside the loop will not be executed and the loop will terminate in the normal fashion from having traversed all $\mathit{\text{n}}$ times. In this case, the function requires $\text{O}\left(n\right)$ time. This is known as the worst case since the function must examine every value in the list requiring the most number of steps.

Now consider the case where the list contains a negative value in the first element:

There will only be one iteration of the loop since the test of the condition by the if statement will be true the first time through and the return statement inside the loop will be executed. In this case, the findNeg function only requires $\text{O}\left(1\right)$ time. This is known as the best case since the function only has to examine the first value in the list requiring the least number of steps.

The average case is evaluated for an expected data set or how we expect the algorithm to perform on average. For the findNeg function, we would expect the search to iterate halfway through the list before finding the first negative value, which on average requires $n⁄2$ iterations. The average case is more difficult to evaluate because it's not always readily apparent what constitutes the average case for a particular problem.

In general, we are more interested in the worst case time-complexity of an algorithm as it provides an upper bound over all possible inputs. In addition, we can compare the worst case run times of different implementations of an algorithm to determine which is the most efficient for any input.