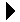2.6 Maintaining Ordered Data

The Polygon ADT is an example of a mutable ordered sequence. An ordered sequence is a container in which the elements are arranged in linear order from front to back. When the elements of the sequence are accessible by position, as is the case with the Polygon ADT, it is normally referred to as an indexed ordered sequence or simply an indexed sequence. Throughout the text, we assume that access to the individual elements of an indexed sequence is based on their position within the linear order, which is provided using the subscript operator.

Since a polygon is defined by an arbitrary number of vertices ($>\; 3$) we will need a way to store the vertices within an instance of the Polygon class. The obvious choice is to represent each vertex using a Point storage object as we did in Section 1.10 for the second implementation of the line segment

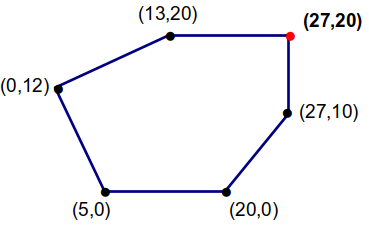
and to store the objects within a list. For example, suppose we want to create the following polygon

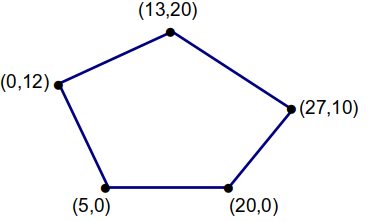
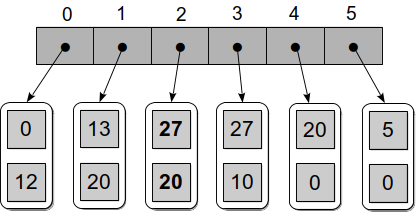
then we will need to store a collection of Point objects within a list structure as shown below

Unlike the Bag ADT introduced earlier in the chapter, the elements contained in a polygon must be stored or arranged in a specific order. Given the list of points that define the vertices, edges of the polygon are defined between successive points with the last edge formed between the last entry in the list and the first. In addition, we must be able to access the individual vertices by position or index. This is easily done, since the elements of a list structure can themselves be accessed by position.

The Constructor

To implement the Polygon class, we begin with the constructor. The constructor takes six arguments, two for each of the three pairs of vertex coordinates. The vertices will be stored in Point objects within a list. The order in which the vertices are added to the list is important, they must follow the order provided in the argument list.

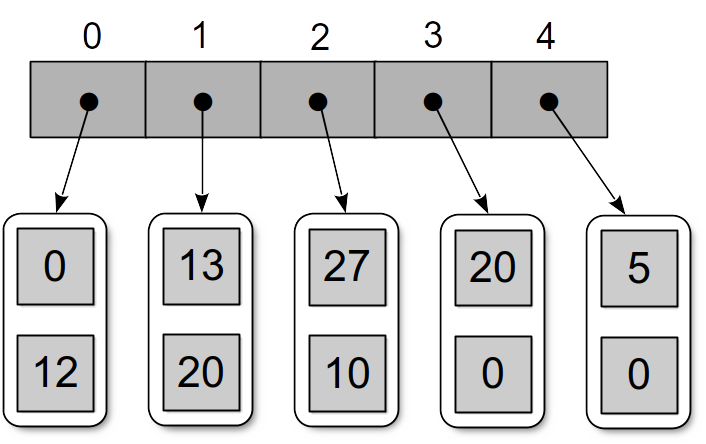
A sample instance of the Polygon class is illustrated below

Number of Vertices

Since we are using a list to store the Point objects, one for each vertex, the number of vertices that define the polygon can be obtained from the length of the list.

Finding a Vertex

Accessing the vertex at a given index position is simply a matter of accessing the corresponding element in the list. Of course, we have to check the precondition before attempting to element the list element:

The findVertex method is suppose to find and return the index position for a given vertex. While Python's list container includes an index method for just this purpose, we can not use it since the vertices are stored in the list using Point objects. Instead, we have to implement our own search:

Inserting a Vertex

The insertVertex method allows us to modify a polygon by inserting a new vertex at any position between two existing vertices. For example, suppose we want to insert a new vertex $(27,\; 20)$ into our sample polygon at index position 2, which is between vertices $(13,\; 20)$ and $(27,\; 10)$.

Then we would supply the statement

To accomplish this, the method should create a Point object for the new vertex and insert it at the given index position using the insert method on the list. If the index is equal to the number of vertices in the list, then we can simply append it to the end of the list.

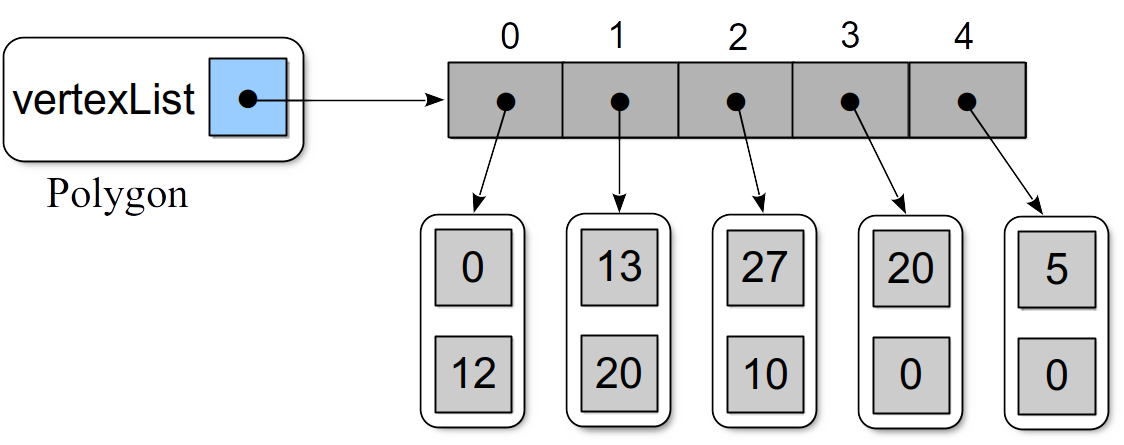
The resulting list after inserting the new vertex would look as follows:

The insertVertex method has two preconditions that must be checked before the new vertex can be added to the list: the index must be within range and the new vertex can not be identical to an existing vertex:

The full implementation of the insertVertex method follows:

The complete implementation of the Polygon class is provided in the source listing below. The implementation of the remaining methods are left as an exercise.