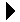6.11 Improved Set Implementation

On this page...

New Set Equals Method
New Set Union Method
Comparing the Set Implementations

In the previous section, we used a sorted list and the binary search to provide an alternative implementation for the Set ADT. That implementation provided better time-complexities for several of the operations, but we only achieved a time of $O (n log n)$ for the subset and equals operations and maintained the same quadratic time for the set union, intersection, and difference operations. A more efficient implementation is possible if we take into account that we know the underlying lists of the two sets are in sorted order and work directly with the sorted lists instead of calling various set operations.

New Set Equals Method

For the set equals operation, instead of calling the isSubsetOf method to determine if the two sets are equal, what if we simply compared the elements of the two lists directly? Remember, for two sets to be equal, they must contain the exact same elements. Since the lists for both sets are sorted, not only must they contain the same elements, but those elements must be in corresponding positions within the two lists for the sets to be equal. Suppose we create three sets, all of which are of the same length, two of which are equal

setA = Set()

setA.add(7)

setA.add(15)

setA.add(38)

setA.add(24)

setB = Set()

setB.add(24)

setB.add(19)

setB.add(45)

setB.add(7)

setC = Set()

setC.add(15)

setC.add(38)

setC.add(24)

setC.add(7)

The physical view of the three sets are illustrated in Figure 6.11.1. Take a moment and observe the elements within each of the sorted lists.

Figure 6.11.1: The physical view for three sample sets implemented using sorted lists.

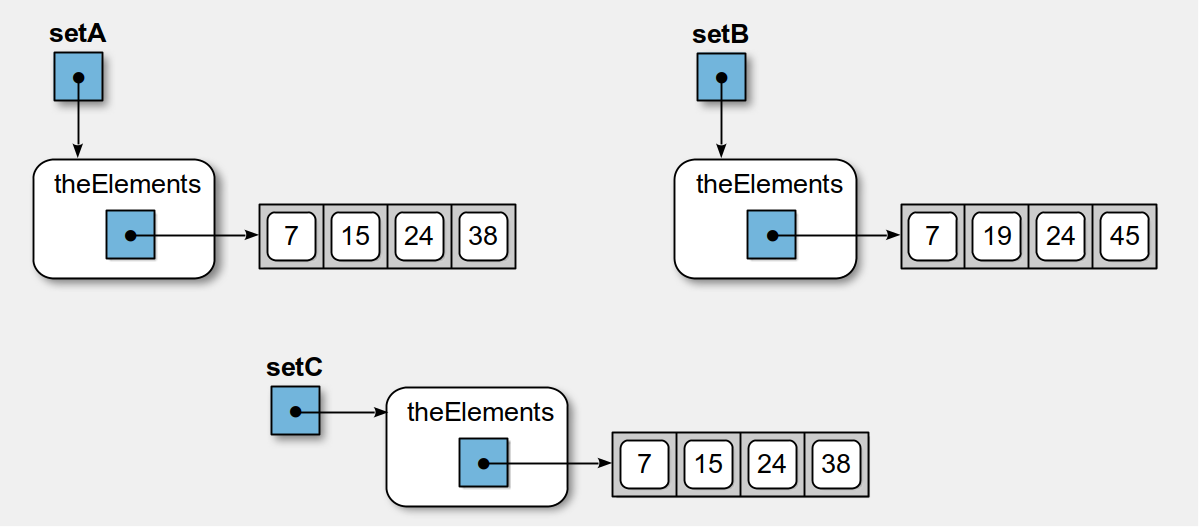
If we compare setA with setC

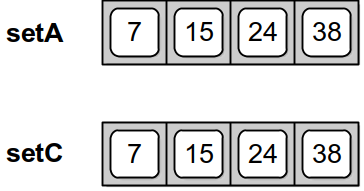
you can see that the two lists have the same size and all of the elements are in corresponding positions. Here, the two sets are equal. On the other hand, if we compare setA with setB

the two lists are of the same size, but notice that the corresponding elements in the second position are not equal. Hence, the two sets can not be equal.

A new implementation of the set equals operation is provided below. The two lists are traversed simultaneously during which corresponding elements are compared. If a single instance occurs where corresponding elements are not identical, then the two sets cannot be equal. Otherwise, having traversed the entire list and finding no mismatched items, the two sets must be equal.

Program Listing

Program: equals.py

class Set :
# ...
def __eq__(self, setB) :
if len(self) != len(setB) :
return False
else :
for i in range( len(self) ) :
if self._theElements[i] != setB._theElements[i] :
return False
return True

The new implementation only requires $O (n)$ time since it only involves one complete simultaneous traversal of the two lists. A similar approach can be used to improve the efficiency of the isSubsetOf method to only require $O (n)$ time, which is left as an exercise.

New Set Union Method

The efficiency of the set union operation can also be improved from the original version. Set union using two sorted lists is very similar to the problem of merging two sorted lists that was introduced in the previous section. In that problem, the entire contents of the two sorted lists were merged into a third list. For the Set ADT implemented using a sorted list, the result of the set union must be a new sorted list merged from the unique values contained in the sorted lists used to implement the two source sets.

The implementation of the new union method uses a modified version of the mergeSortedLists function from Section 6.9. The only modification required is the inclusion of an additional test within the first loop to catch any duplicate values by advancing both index variables and only appending one copy to the new sorted list. The new implementation only requires $O (n)$ time since that is the time required to merge two sorted lists and the new test for duplicates does not increase that complexity. The set difference and set intersection operations can also be modified in a similar fashion and are left as an exercise.

Program Listing

Program: union.py

class Set :
# ...
def union(self, setB):
newSet = Set()
a = 0
b = 0
# Merge the two lists together until one is empty.
while a < len(self) and b < len(setB) :
valueA = self._theElements[a]
valueB = setB._theElements[b]
if valueA < valueB :
newSet._theElements.append(valueA)
a += 1
elif valueA > valueB :
newSet._theElements.append(valueB)
b += 1
else : # Only one of the two duplicates are appended.
newSet._theElements.append(valueA)
a += 1
b += 1
# If listA contains more items, append them to newList.
while a < len(self) :
newSet._theElements.append(self._theElements[a])
a += 1
# Or if listB contains more, append them to newList.
while b < len(setB) :
newSet._theElements.append(setB._theElements[b])
b += 1
return newSet

Comparing the Set Implementations

The implementation of the Set ADT using an unsorted list was quick and easy, but after evaluating the various operations, it became apparent many of them were time consuming. A new implementation using a sorted list to store the elements of the set and the binary search algorithm for locating elements improved the contains operation. This resulted in better times for the isSubsetOf and set equals operations, but the set union, intersection, and difference operations remained quadratic. After observing several operations could be further improved if they were implemented to directly access the list instead of using the contains operation, we were able to provide a more efficient implementation of the Set ADT. Table 6.11.1 compares the worst case time-complexities for the Set ADT operations using an unsorted list and the improved sorted list version using the binary search and the list merging operation.

Set Operation	Original (1)	Improved (2)	Efficient (3)
`s = Set()`	$O (1)$	$O (1)$	$O (1)$
`len(s)`	$O (1)$	$O (1)$	$O (1)$
`x in s`	$O (n)$	$O (log n)$	$O (log n)$
`s.add(x)`	$O (n)$	$O (n)$	$O (n)$
`s.isSubsetOf(t)`	$O (n^{2})$	$O (n log n)$	$O (n)$
`s == t`	$O (n^{2})$	$O (n log n)$	$O (n)$
`s.union(t)`	$O (n^{2})$	$O (n^{2})$	$O (n)$

Table 6.11.1: Comparison of the three Set ADT implementations: (1) the original version using an unsorted list, (2) the improved version using a sorted list with a binary search, and (3) the efficient implementation using a sorted list and list merging.

6.10 The Set ADT Revisited

Chapter 6. Searching and Sorting

Chapter Exercises