8.6 Bounded Priority Queue

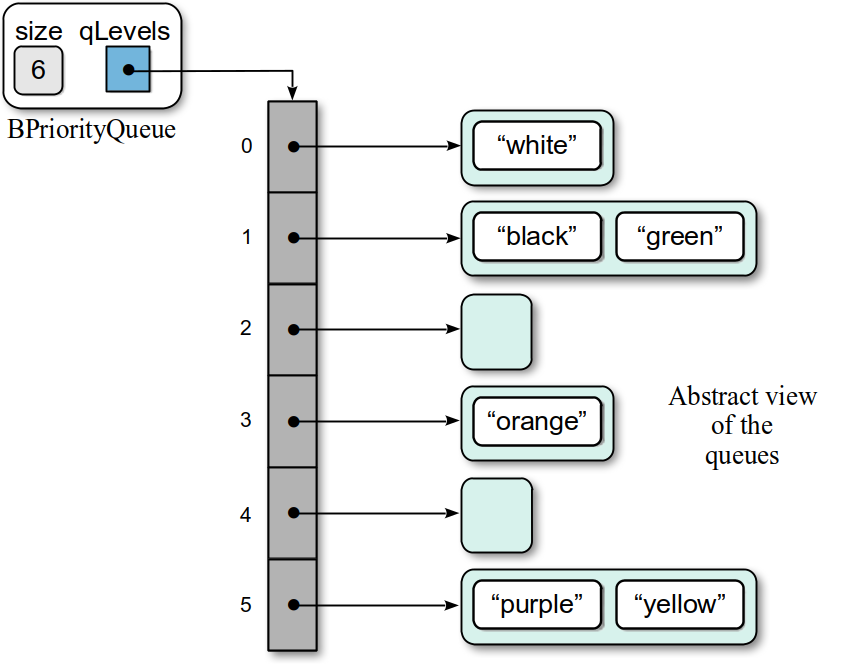
The Python list and linked list versions are quite simple to implement and can be used to implement the bounded priority queue. But they both require linear time to dequeue an item. Since the priorities of a bounded priority queue are restricted to a finite set $[0 \dots p)$ , we can improve this worst case time with an implementation in which all of the operations only require constant time. This can be done using an array of queues, as illustrated in Figure 8.6.1.

Figure 8.6.1: Implementation of the priority queue using an array of queues.

The constructor for the bounded priority queue requires an argument indicating the number of priority levels. Thus, we use a different class name (BPriorityQueue) to differentiate it from the unbounded priority queue. The constructor creates two data fields:

class BPriorityQueue :

  def __init__(self, numLevels):

    self._qSize = 0

    self._qLevels = Array(numLevels)

    for i in range(numLevels) :

      self._qLevels[i] = Queue()

The _qLevels field contains an array of $p$ elements in which each contains an instance of the Queue ADT. The _size field maintains the number of items in the priority queue and is used by the __len__ operation:

def __len__(self) :

  return self._qSize

The _size field can also be used to determine if the queue is empty:

def isEmpty(self) :

  return self._qSize == 0    

When an item with priority $k$ is added to the priority queue, it is added to the queue stored in the qList[k] element. Before adding the new item, however, we must first ensure the priority is within the valid range. The implementation of the enqueue operation follows:

def enqueue(self, item, priority) :

  assert priority >= 0 and priority < len(self._qLevels),

         "Invalid priority level."

  self._qLevels[priority].enqueue( item )

To dequeue an item from the priority queue, we must iterate through the array to find the first non-empty queue, which will contain the first item to be removed from the priority queue.

def dequeue(self) :

  assert not self.isEmpty(), "Cannot dequeue from an empty queue."    

  i = 0

  p = len(self._qLevels)    

  while i < p and not self._qLevels[i].isEmpty() :

    i += 1

  return self._qLevels[i].dequeue()

Note that we do not have to store the priorities along with each item since all items with a given priority will be stored in the same queue. The priority can be determined from the array indices. The complete implementation of the bounded Priority Queue ADT is shown in the listing below.

Program Listing

Program: bpriorityq.py

# Implementation of the bounded Priority Queue ADT using an array of
# queues in which the queues are implemented using a linked list.
from ezarrays import Array
from llistqueue import Queue
class BPriorityQueue :
# Creates an empty bounded priority queue.
def __init__(self, numLevels):
self._qSize = 0
self._qLevels = Array(numLevels)
for i in range(numLevels) :
self._qLevels[i] = Queue()
# Returns True if the queue is empty.
def isEmpty(self) :
return self._qSize
# Returns the number of items in the queue.
def __len__(self) :
return self._qSize
# Adds the given item to the queue.
def enqueue(self, item, priority) :
assert priority >= 0 and priority < len(self._qLevels),
"Invalid priority level."
self._qLevels[priority].enqueue( item )
# Removes and returns the next item in the queue.
def dequeue(self) :
# Make sure the queue is not empty.
assert not self.isEmpty(), "Cannot dequeue from an empty queue."
# Find the first non-empty queue.
i = 0
p = len(self._qLevels)
while i < p and not self._qLevels[i].isEmpty() :
i += 1
# We know the queue is not empty, so dequeue from the ith queue.
return self._qLevels[i].dequeue()

The implementation of the priority queue using an array of queues is also quite simple. But can we obtain constant time operations? We begin with the isEmpty and __len__ operations. Since a data field is maintained to store the number of items in the priority queue, both can be performed in constant time. The enqueue operation also requires constant time since adding an item to a general queue can be done in constant time as can accessing an individual queue in the array. Dequeuing from a general queue implemented as a linked list can be done in constant time. But since we must iterate through the array to find the first non-empty queue, the priority dequeue operation requires $O (p)$ time. While this time is linear, it is linear with respect to the number of priorities and not to the number of elements in the queue ( $n$ ). When the number of priorities is quite small, we can safely treat $p$ as a constant value and specify the dequeue operation as requiring constant time.

The disadvantage of this structure for the implementation of the priority queue is that the number of levels is fixed. If an application requires a priority queue with an unlimited number of priority levels, then the vector or linked-list versions are a better choice.

8.5 Unbounded Priority Queue

Chapter 8. Queues

8.7 Application: Computer Simulations