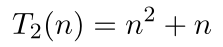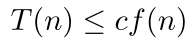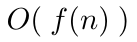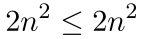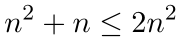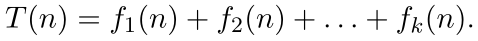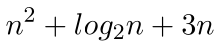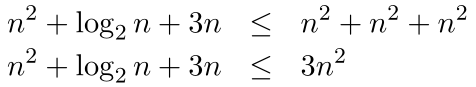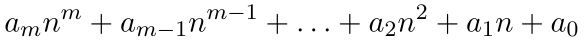5.2 Big-O Notation

Instead of counting the precise number of operations or steps, computer scientists are more interested in classifying an algorithm based on the order of magnitude as applied to execution time or space requirements. This classification approximates the actual number of required steps for execution or the actual storage requirements in terms of variable-sized data sets. The term big-O, which is derived from the expression "on the order of," is used to specify an algorithm's classification.

Defining Big-O

Assume we have a function $\mathit{\text{T(n)}}$ that represents the approximate number of steps required by an algorithm for an input of size $\mathit{\text{n}}$. For the second version of our algorithm in the previous section, this would be written as

Now, suppose there exists a function $\mathit{\text{f(n)}}$ defined for the integers $n\ge 0$, such that for some constant $\mathit{\text{c}}$, and some constant $\mathit{\text{m}}$,

for all sufficiently large values of $n\ge m$. Then, such an algorithm is said to have a time-complexity of, or executes on the order of, $\mathit{\text{f(n)}}$ relative to the number of operations it requires. In other words, there is a positive integer $\mathit{\text{m}}$ and a constant $\mathit{\text{c}}$ (constant of proportionality) such that for all $\mathit{\text{n ≥ m}}$, $\mathit{\text{T(n) ≤ c f(n)}}$. The function $\mathit{\text{f(n)}}$ indicates the rate of growth at which the run time of an algorithm increases as the input size, $\mathit{\text{n}}$, increases. To specify the time-complexity of an algorithm, which runs on the order of $\mathit{\text{f(n)}}$, we use the notation

Consider the two versions of our algorithm from earlier. For version one, the time was computed to be $T_1(n)=2n^2$. If we let $\mathit{\text{c = 2}}$, then

for a result of $\text{O}\left(n^2\right)$. For version two, we computed a time of $T_2(n)=n^2+n$. Again, if we let $\mathit{\text{c = 2}}$, then

for a result of $\text{O}\left(n^2\right)$. In this case, the choice of $\mathit{\text{c}}$ comes from the observation that when $\mathit{\text{n ≥ 1}}$, we have $n\le n^2$ and $n^2+n\le n^2+n^2$, which satisfies the equation in the definition of big-O.

The function $\mathit{\text{f(n) = n²}}$ is not the only choice for satisfying the condition $\mathit{\text{T(n) ≤ c f(n)}}$. We could have said the algorithms had a run time of $\text{O}\left(n^3\right)$ or $O\left(n^4\right)$ since $\mathit{\text{2n² ≤ n³}}$ and $\mathit{\text{2n² ≤ n⁴}}$ when $\mathit{\text{n > 1}}$. The objective, however, is to find a function $\mathit{\text{f(·)}}$ that provides the tightest (lowest) upper bound or limit for the run time of an algorithm. The big-O notation is intended to indicate an algorithm's efficiency for large values of $\mathit{\text{n}}$. There is usually little difference in the execution times of algorithms when $\mathit{\text{n}}$ is small.

Constant of Proportionality

The constant of proportionality is only crucial when two algorithms have the same $\mathit{\text{f(n)}}$. It usually makes no difference when comparing algorithms whose growth rates are of different magnitudes. Suppose we have two algorithms, $\mathit{\text{L₁}}$ and $\mathit{\text{L₂}}$, with run times equal to $\mathit{\text{n²}}$ and $\mathit{\text{2n}}$ respectively. $\mathit{\text{L₁}}$ has a time-complexity of $\text{O}\left(n^2\right)$ with $\mathit{\text{c = 1}}$ and $\mathit{\text{L₂}}$ has a time of $\text{O}\left(n\right)$ with $\mathit{\text{c = 2}}$. Even though $\mathit{\text{L₁}}$ has a smaller constant of proportionality, $\mathit{\text{L₁}}$ is still slower and, in fact an order of magnitude slower for large values of $\mathit{\text{n}}$. Thus, $\mathit{\text{f(n)}}$ dominates the expression $\mathit{\text{c f(n)}}$ and the run time performance of the algorithm. The differences between the run times of these two algorithms is shown numerically in Table 5.2.1 and graphically in Figure 5.2.1.

Figure 5.2.1: Graphical comparison of the data from Table 5.1.2

Constructing T(n)

Instead of counting the number of logical comparisons or arithmetic operations, we evaluate an algorithm by considering every operation. For simplicity, we assume that each basic operation or statement, at the abstract level, takes the same amount of time and, thus, each is assumed to cost constant time. The total number of operations required by an algorithm can be computed as a sum of the times required to perform each step:

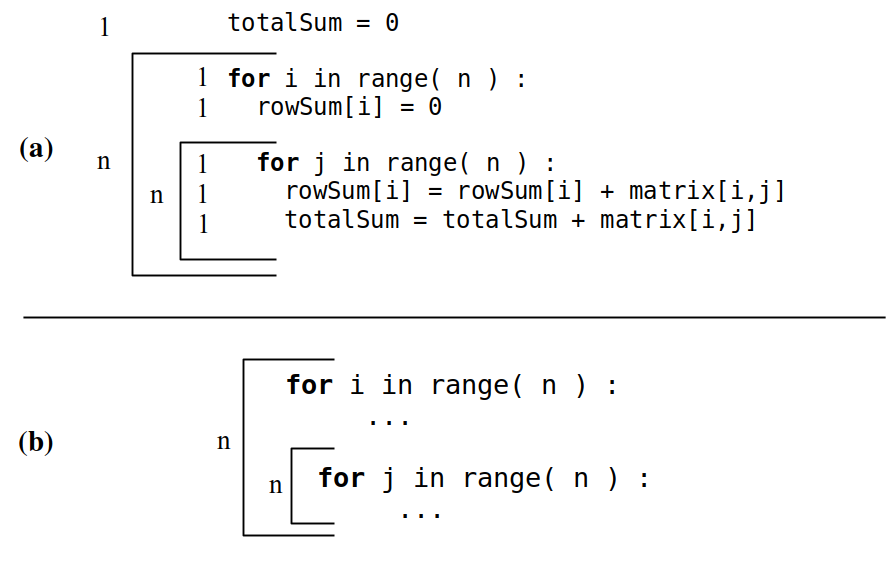
The steps requiring constant time are generally omitted since they eventually become part of the constant of proportionality. Consider Figure 5.2.2 (a), which shows a markup of version one of the algorithm from earlier. The basic operations are marked with a constant time while the loops are marked with the appropriate total number of iterations. Figure 5.2.2 (b) shows the same algorithm but with the constant steps omitted since these operations are independent of the data set size.

Figure 5.2.2: Markup for version one of the matrix summing algorithm: (a) all operations are shown, and (b) only the non-constant time steps are shown.

Choosing the Function

The function $\mathit{\text{f(n)}}$ used to categorize a particular algorithm is chosen to be the dominant term within $\mathit{\text{T(n)}}$. That is, the term that is so large for big values of $\mathit{\text{n}}$, that we can ignore the other terms when computing a big-O value. For example, in the expression

the term $\mathit{\text{n²}}$ dominates the other terms since for $\mathit{\text{n ≥ 3}}$, we have

which leads to a time-complexity of $\text{O}\left(n^2\right)$. Now, consider the function $\mathit{\text{T(n) = 2n² + 15n + 500}}$ and assume it is the polynomial that represents the exact number of instructions required to execute some algorithm. For small values of $\mathit{\text{n}}$ (less than 16), the constant value $\mathit{\text{500}}$ dominates the function, but what happens as $\mathit{\text{n}}$ gets larger, say $\mathit{\text{100,000}}$? The term $\mathit{\text{n²}}$ becomes the dominant term, with the other two becoming less significant in computing the final result.

Classes of Algorithms

We will work with many different algorithms in this text, but most will have a time-complexity selected from among a common set of functions, which are listed in Table 5.2.2 and illustrated graphically in Figure 5.2.3.

Algorithms can be classified based on their big-O function. The various classes are commonly named based upon the dominant term. A logarithmic algorithm is any algorithm whose time-complexity is $O({\log }_{a}n)$. These algorithms are generally very efficient since ${\log }_{a}n$ will increase more slowly than $\mathit{\text{n}}$. For many problems encountered in computer science $\mathit{\text{a}}$ will typically equal 2 and thus we use the notation $\log n$ to to imply ${\log }_{2}n$. Logarithms of other bases will be explicitly stated. Polynomial algorithms with an efficiency expressed as a polynomial of the form

are characterized by a time-complexity of $O(n^m)$ since the dominant term is the highest power of $\mathit{\text{n}}$. The most common polynomial algorithms are linear ($\mathit{\text{m = 1}}$), quadratic ($\mathit{\text{m = 2}}$), and cubic ($\mathit{\text{m = 3}}$). An algorithm whose efficiency is characterized by a dominant term in the form $\mathit{\text{aⁿ}}$ is called exponential. Exponential algorithms are among the worst algorithms in terms of time-complexity.

Figure 5.2.3: Growth rates of the common time-complexity functions.