8.2 Queue Implementation

On this page...

Python List Implementation
Linked List Implementation

Since the queue data structure is simply a specialized list, it is commonly implemented using some type of list structure. There are three common approaches to implementing a queue: using a vector, a linked list, or an array. In the following sections, we examine and compare these three approaches.

Python List Implementation

The simplest way to implement the Queue ADT is to use Python's list. It provides the necessary routines for adding and removing items at the respective ends. By applying these routines, we can remove items from the front of the list and append new items to the end. To use a list for the Queue ADT, the constructor must define a single data field to store the list that is initially empty:

class Queue :

  def __init__(self) :

    self._qList = list()

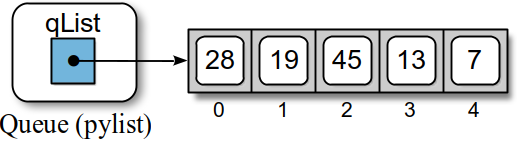
Figure 8.2.1 illustrates an instance of the class for the queue from Figure 8.1.1.

Figure 8.2.1: An instance of the Queue ADT implemented using a Python list.

We can test for an empty queue and obtain the size of the queue by examining the length of the list:

def isEmpty(self) :

  return len(self._qList) == 0

def __len__(self) :

  return len(self._qList)

To enqueue an item, we simply append the item to the end of the list:

def enqueue(self, item) :

  self._qList.append(item)

The dequeue operation can be implemented by popping and returning the item in the first element of the list:

def dequeue(self) :

  assert not self.isEmpty(), "Can not dequeue from an empty queue."

  return self._qList.pop(0)

Before attempting to remove an item from the list, we must ensure the queue is not empty. Remember, the queue definition prohibits the use of the dequeue operation on an empty queue. Thus, to enforce this, we must first assert the queue is not empty and raise an exception, when the operation is attempted on an empty queue. The complete Python list-based implementation is provided in the listing below.

Program Listing

Program: pylistqueue.py

# Implementation of the Queue ADT using a Python list.
class Queue :
# Creates an empty queue.
def __init__(self) :
self._qList = list()
# Returns True if the queue is empty.
def isEmpty(self) :
return len(self._qList) == 0
# Returns the number of items in the queue.
def __len__(self) :
return len(self._qList)
# Adds the given item to the queue.
def enqueue(self, item) :
self._qList.append(item)
# Removes and returns the first item in the queue.
def dequeue(self):
assert not self.isEmpty(), "Can not dequeue from an empty queue."
return self._qList.pop(0)

Since we use list operations to implement the individual queue operations, we need only recall the worst case times for the Python list operations. The size and empty condition operations only require $O (1)$ time. The enqueue operation requires $O (n)$ time in the worst case since the list may need to expand to accommodate the new item. When used in sequence, the enqueue operation has an amortized cost of $O (1)$ . The dequeue operation also requires $O (n)$ time since the underlying array used to implement the Python list may need to shrink when an item is removed. In addition, when an item is removed from the front of the list, the following items have to be shifted forward, which requires linear time no matter if an expansion occurs or not. Table 8.2.1 provides a summary of the worst case time-complexities for a queue implemented using a Python list.

Operation	Worst Case
`q = Queue()`	$O (1)$
`len(q)`	$O (1)$
`q.isEmpty()`	$O (1)$
`q.enqueue(item)`	$O (n)$
`x = q.dequeue()`	$O (n)$

Table 8.2.1: Time-complexities for the Queue implemented using a Python list.

Linked List Implementation

A major disadvantage in using a Python list to implement the Queue ADT is the expense of the enqueue and dequeue operations. A better solution is to use a linked list consisting of both head and tail references. Adding the tail reference allows for quick append operations that otherwise would require a complete traversal to find the end of the list. Figure 8.2.2 illustrates a sample linked list with the two external references.

Figure 8.2.2: An instance of the Queue ADT implemented as a linked list.

The complete implementation of the Queue ADT using a linked list with a tail reference is provided in the listing below. Remember, the individual nodes in the list contain the individual items in the queue. When dequeuing an item, we must unlink the node from the list but return the item stored in that node and not the node itself. An evaluation of the time-complexities is left as an exercise.

Program Listing

Program: llistqueue.py

# Implementation of the Queue ADT using a linked list.
class Queue :
# Creates an empty queue.
def __init__(self) :
self._qhead = None
self._qtail = None
self._count = 0
# Returns True if the queue is empty.
def isEmpty(self) :
return self._qhead is None
# Returns the number of items in the queue.
def __len__(self) :
return self._count
# Adds the given item to the queue.
def enqueue(self, item) :
node = QueueNode(item)
if self.isEmpty() :
self._qhead = node
else :
self._qtail.next = node
self._qtail = node
self._count += 1
# Removes and returns the first item in the queue.
def dequeue(self) :
assert not self.isEmpty(), "Cannot dequeue from an empty queue."
node = self._qhead
if self._qhead is self._qtail :
self._qtail = None
self._qhead = self._qhead.next
self._count -= 1
return node.item
# Private storage class for creating the linked list nodes.
class QueueNode :
def __init__(self, item) :
self.item = item
self.next = None

8.1 The Queue ADT

Chapter 8. Queues

8.3 Circular Array Implementation