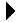7.9 The Sorted Linked List

The items in a linked list can be sorted in ascending or descending order as was done with a sequence. Consider the sorted linked list illustrated in Figure 7.9.1. The sorted list has to be created and maintained as items are added and removed.

Figure 7.9.1: A sorted linked list with items in ascending order.

Linear Search

The linear search for use with the linked list can be modified to take advantage of the sorted items. The only change required is to add a second condition that terminates the loop early if we encounter a value larger than the target. The search routine for a sorted linked list is shown in the listing below.

Inserting Nodes

Adding a new node to an unsorted linked list is simple because we can simply add it to the front or end of the list since its placement is not important. When adding a node to a sorted list, however, the correct position for the new value must be found and the new node linked into the list at that position. The Python implementation for inserting a value into a sorted linked list is provided below.

As with the removal operation for the unsorted list, we must position two temporary external references by traversing through the linked list searching for the correct position of the new value. The only difference is the loop termination condition. To insert a new node, we must terminate the loop upon finding the first value larger than the new value being added.

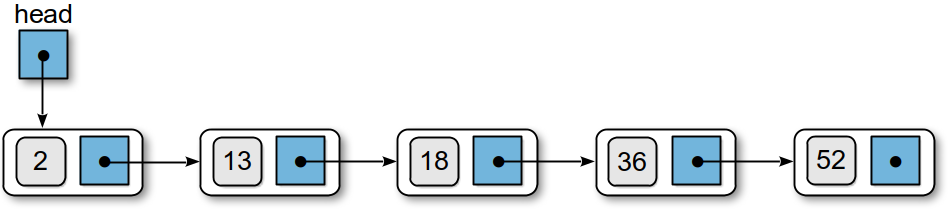
Three cases can occur when inserting a node into a sorted linked list, as illustrated in Figure 7.9.2: the node is inserted in the front, at the end, or somewhere in the middle. After finding the correct position, a new node is created and its next field is changed to point to the same node referenced by curNode. This link is required no matter where in the list the new node is inserted. If the new node is to be inserted in the front, then the operation is a simple prepend, as was done with an unsorted linked list, and curNode will be pointing to the first node. When the new value being added is the largest in the list and the new node is to be added at the end, curNode will be null and thus the next field will be null as it should be. When the new node is inserted elsewhere in the list, curNode will be pointing to the node that will follow the new node.

Figure 7.9.2: Inserting a new value into a sorted linked list: (a) inserting -7 at the front of the list; (b) inserting 24 in the middle of the list; (c) inserting 69 at the end of the list.

After linking the new node to the list, we must determine if it is being inserted at the front of the list, in which case the head reference must be adjusted. We do this by comparing the curNode reference with the head reference. If they are aliases, the new node comes first in the linked list and we must adjust the head reference to point to the new node. If the two nodes are not aliases, then the node is inserted by setting the next field of the node referenced by predNode to point to the new node.

Traversing and Deleting

The traversal operation implemented for the unsorted linked list can be used with both sorted and unsorted linked lists since it is not dependent on the contents of the list itself. Deleting from a sorted linked list is the same operation used with an unsorted list with one exception. Searching for the node containing the target value can end early after encountering the first value larger than the one to be deleted.