5.7 Set Operations

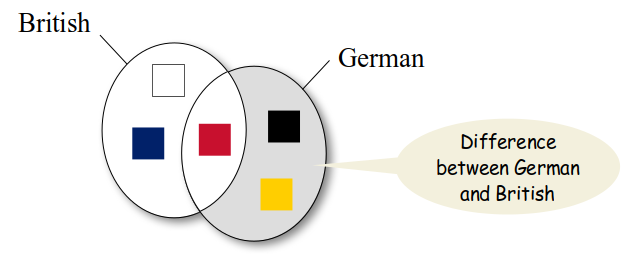
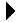Sets can be used to solve a variety of problems. Suppose we have a collection of flags for various countries in Europe and we would like to answer questions related to the colors used in those flags. For example, we could ask how many of the flags share a common color (or similar shade of color)? Or, what is the set of unique colors used across all of the flags? To help answer these questions, we can construct a set of colors for each flag as illustrated in Figure 5.7.1 and then apply one or more set operations to the sets.

Figure 5.7.1: Sample sets of flag colors.

In mathematics, a set is indicated by enclosing the elements of the set within curly braces. Thus, we could specify the sets for our four flags shown above as follows:

finnish = {"blue", "white"}
french = {"blue", "red", "white"}
british = {"red", "white", "blue"}
german = {"black", "red", "gold"}

Creating Sets

Although Python does provide a set container as part of the language itself, we are going to review the operations as defined by the Set ADT from the previous section, since you will later be asked to implement it. Thus, all of the code examples rely on that abstract data type definition instead of Python's built-in set type.

To create a set using our Set ADT, we can not use the mathematical notation. Instead, we must start with an empty set

and then add elements to the set using the add method

Since the elements are not stored in any particular order, the order in which the elements are added does not matter. We can then add the two additional colors for the British flag:

The elements of a set must be unique. If the element being added is not already contained in the set, it will be added and the set size increased by one. If you attempt to add an element that is already in the set, there is no effect and the set is not changed.

To create the set of colors for the other three flags, we would follow the same steps

Using Sets

As with other containers in Python, you can use the len function to determine the size of a set

A set that contains no elements is called the empty set. The isEmpty method can be used to check for this condition:

To determine whether an element is contained in the set, use the in operator or its inverse, the not in operator:

Because sets are unordered, you cannot access the elements of a set by position. Instead, you can use the for loop to iterate over the individual elements:

Note the order in which the elements of the set are visited depends on how they are stored internally. The loop above would produce output similar to the following:

Colors of the French flag:
blue
white
red

The fact that sets do not retain the initial ordering is not a problem when working with sets. In fact, it allows for a more efficient implementation than is possible with a vector.

Removing Elements

Elements can be removed from a set using the remove method. Suppose we are creating our own flag and start with three colors in a set:

which is represented graphically as

Later, we decide that we want to swap the red for gold. To accomplish this, we first remove the red element from the set

which results in the set now having two elements

The element being removed must be contained in the set, otherwise an exception is raised. Thus, it is good practice to first determine if the element is in the set before attempting to remove it

Having removed the red color, we can now add a new element for gold,

to produce our final set of three colors

Subsets

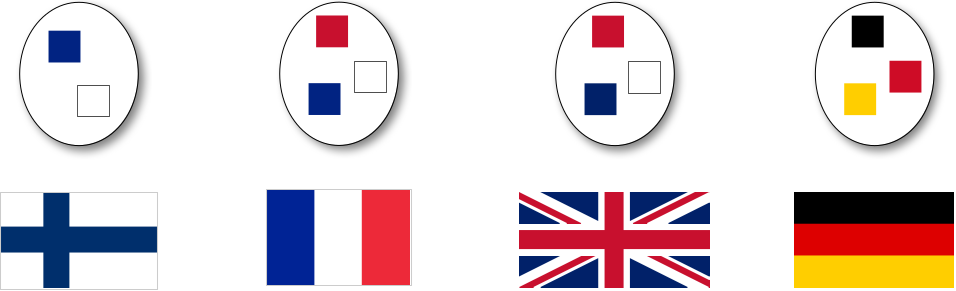
The Set ADT includes operations that can be used to determine the relationship between two sets. A set is a subset if an only if every element of the first set is also an element of the second set. Consider the sets of flag colors in Figure 5.7.1 above. The Finnish colors are a subset of the British colors as shown below

but the German colors are not a subset of the British colors

The isSubsetOf method returns a Boolean to indicate whether one set is a subset of another. Assume we have defined the following sets:

We can test our observations from above using the following code:

You can also test whether two sets are equal using the == and != operators. Two sets are equal if and only if they contain the exact same elements. Suppose we create a set representing the colors in the French flag, we can then determine if the flag has the same colors as either the British or Finnish flags:

Question 5.7.2

Consider the colors in the Italian flag

Is the set of Italian flag colors a subset of any of the four flags shown in Figure 5.7.1?

Select the correct answer below by clicking on the appropriate box.

1. Yes
2. No

While the Italian flag shares one or two colors, red and white, with the other flags, none of the other flags also contain green. Thus, it can not be a subset of any of the other sets of colors.

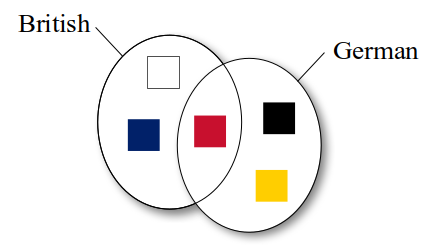
Set Union

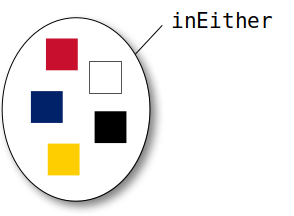
The Set ADT also provide operations that create and return new sets. The union of two sets contains all of the elements from both sets, with no duplicates. Consider the union of the individual colors for the french and german flags:

The union method is used to create the union of two sets:

which results in a new set

that contains one instance of each color from both flags. Both the french and german flags contain the color "red", but the union operation creates a new a set and therefore contains only one instance of each color.

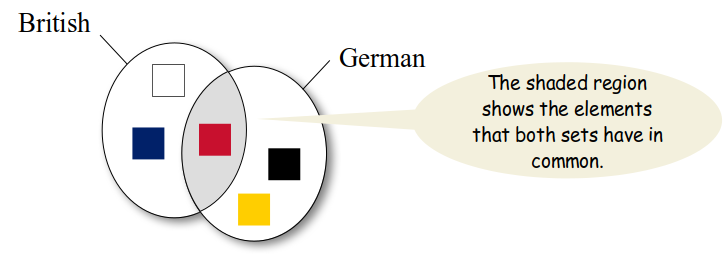
Set Intersection

The intersection of two sets contains all of the elements that are in both sets. The result is a new set that tells us what the two sets have in common. For example, if we perform a set intersection on the two sets representing the colors of the British and German flags,

we can see what colors the two flags have in common

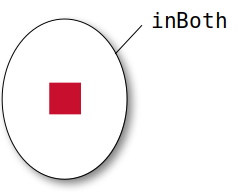
The set intersection is performed using the intersection method

Question 5.7.4

If we perform the set intersection on the two sets representing the colors in the German and Finnish flags, how can we determine that the two flags have no colors in common?

If the two sets have no elements in common, the resulting set will be empty. Thus, we can use the isEmpty method to check for this condition:

inBoth = german.intersection(finnish)
if inBoth.isEmpty() :
   print("The German and Finnish flags have no colors in common.")

Question 5.7.5

Assume the three colors in the Italian flag

are represented by the set italian. What is the result of performing the set operation

result = italian.intersection(finnish)

Select the correct answer below by clicking on the appropriate box.

1. the empty set
2. a set containing the colors white and blue
3. a set containing the color white
4. a set of four elements for the colors blue, white, red, and green

Set Difference

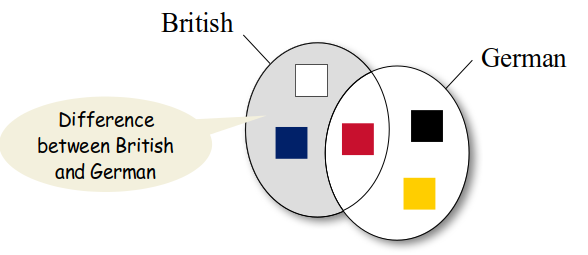
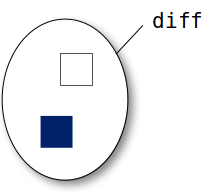
Finally, the difference of two sets results in a new set that contains those elements in the first set that are not in the second set. For example, the difference between the British flag and the German flag

is the set containing only "blue" and "white"

Use the difference method to find the set difference:

When forming the union or intersection of two sets, the order does not matter. For example,

is the same as

But the order matters with the set difference operation. The set returned by

is the set containing "black" and "gold"

Example Program

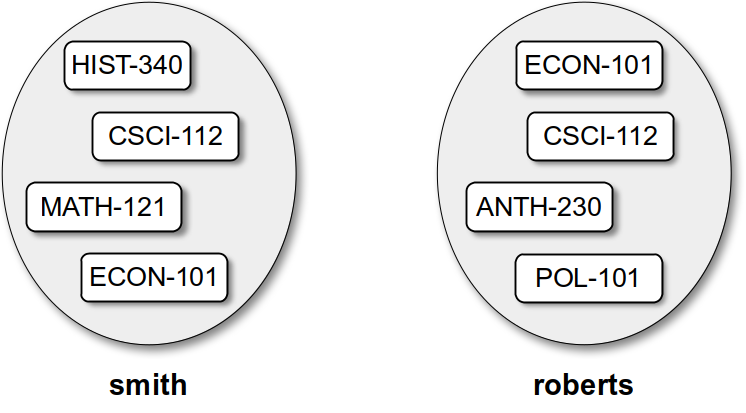
To illustrate the use of the Set ADT, we create and use sets containing the courses currently being taken by two students. In the following code segment,

we create two sets and add elements to each. The results are illustrated in Figure 5.7.2.

Figure 5.7.2: Sample sets representing student schedules.

Next, we determine if the two students are taking the exact same courses. If not, then we want to know if they are taking any of the same courses. We can do this by computing the intersection between the two sets.

In this case, the two students are both taking CSCI-112 and ECON-101. Thus, the results of executing the previous code segment will be

Smith and Roberts are taking some of the same courses:
CSCI-112  ECON-101

Suppose we want to know which courses Smith is taking that Roberts is not taking. We can determine this using the set difference operation:

This example reinforces one of the advantages of working with an abstraction by focusing on what functionality the ADT provides instead of how that functionality is implemented. By hiding the implementation details, we can use an ADT independent of its implementation. In fact, the choice of implementation for the Set ADT will have no effect on the instructions in our example program.