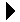Most computer architectures provide a mechanism at the hardware level for creating and using one-dimensional arrays. Programming languages need only provide appropriate syntax to make use of a 1-D array. Multi-dimensional arrays are not handled at the hardware level. Instead, the programming language typically provides its own mechanism for creating and managing multi-dimensional arrays.
As we saw earlier, a one-dimensional array is composed of a group of sequential elements stored in successive memory locations. The index used to reference a particular element is simply the offset from the first element in the array. In most programming languages, a multi-dimensional array is actually created and stored in memory as a one-dimensional array. With this organization, a multi-dimensional array is simply an abstract view of a physical one-dimensional data structure.
Array Storage
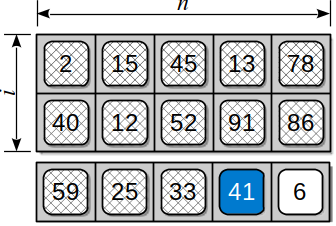
A one-dimensional array is commonly used to physically store arrays of higher dimensions. Consider a two-dimensional array divided into a table of rows and columns as illustrated in Figure 4.5.1. How can the individual elements of the table be stored in the one-dimensional structure while maintaining direct access to the individual table elements? There are two common approaches. The elements can be stored in row-major order or column-major order. Most high-level programming languages use row-major order, with FORTRAN being one of the few languages that uses column-major ordering to store and manage 2-D arrays.
Figure 4.5.1: The abstract view of a sample two-dimensional array.
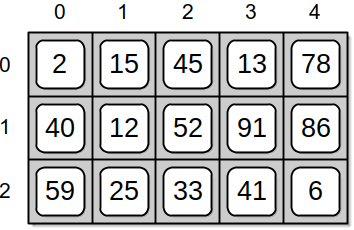
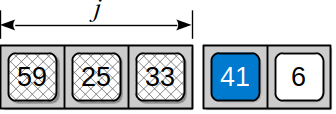
In row-major order, the individual rows are stored sequentially, one at a time, as illustrated in Figure 4.5.2. The first row of 5 elements are stored in the first 5 sequential elements of the 1-D array, the second row of 5 elements are stored in the next five sequential elements, and so forth.
Figure 4.5.2: Physical storage of a sample 2-D array (top) in a 1-D array using row-major order (bottom).
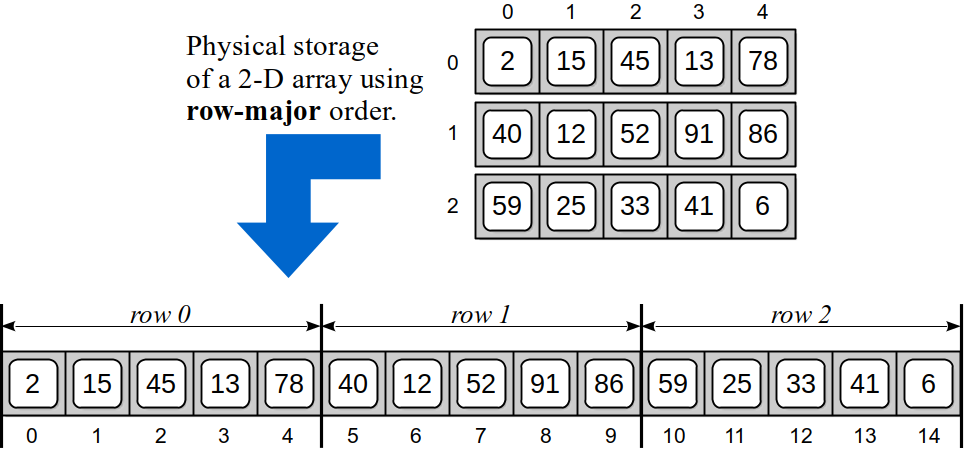
In column-major order, the 2-D array is stored sequentially, one entire column at a time, as illustrated in Figure 4.5.3. The first column of 3 elements are stored in the first 3 sequential elements of the 1-D array, followed by the 3 elements of the second column, and so on.
Figure 4.5.3: Physical storage of a sample 2-D array (top) in a 1-D array using column-major order (bottom).
For larger dimensions, a similar approach can be used. With a three-dimensional array, the individual tables can be stored contiguously using either row-major or column-major ordering. As the number of dimensions grow, all elements within a~single instance of each dimension are stored contiguously before the next instance. For example, given a four-dimensional array, which can be thought of as an array of boxes, all elements of an individual box (3-D array) are stored before the next box.
Index Computation
Since multi-dimensional arrays are created and managed by instructions in the programming language, accessing an individual element must also be handled by the language. When an individual element of a 2-D array is accessed, the compiler must include additional instructions to calculate the offset of the specific element within the 1-D array. Given a 2-D array of size and using row-major ordering, an equation can be derived to compute this offset.
To derive the formula, consider the 2-D array illustrated in Figure 4.5.2 and observe the physical storage location within the 1-D array for the first element in several of the rows. Element maps to position since it is the first element in both the abstract 2-D and physical 1-D arrays. The first entry of the second row maps to position since it follows the first elements of the first row. Likewise, element maps to position since it follows the first elements in the first two rows. We could continue in the same fashion through all of the rows, but you would soon notice the position for the first element of the th row is . Since the subscripts start from zero, the th subscript not only represents a specific row but also indicates the number of complete rows skipped to reach the th row.
Knowing the position of the first element of each row, the position for any element within a 2-D array can be determined. Given an element of a 2-D array, the storage location of that element in the 1-D array is computed as
The column index, , is not only the offset within the given row but also
the number of elements that must be skipped in the th row to reach the th column. To see this formula in action, again consider the 2-D array from Figure 4.5.2 and assume we want to access element . Finding the target element within the 1-D array requires skipping over the first 2 complete rows of elements:
and the first 3 elements within row 2:
Plugging the indices into the equation from above results in an index position of 13, which corresponds to the position of element within the 1-D array used to physically store the 2-D array.
Similar equations can be derived for arrays of higher dimensions. Given a 3-D array of size , the 1-D array offset of element stored using row-major order will be
For each component () in the subscript, the equation computes the number
of elements that must be skipped within the corresponding dimension. For example, the factor indicates the number of elements in a single table of the cube. When it's multiplied by we get the number of complete tables to skip and in~turn the number of elements to skip in order to arrive at the first element of table .
The remaining part of the equation () is equivalent to
which indicates the number of elements to skip within the table. As the number of dimensions increase, additional products are added to the equation, one for each new dimension. For example, the equation to compute
the offset for a 4-D array is
You may notice a pattern developing as the number of dimensions increase. This pattern leads to a general equation for computing the 1-D array offset for element within an -dimensional array:
where the values are the factors representing the number of elements to be skipped within the corresponding dimension and are computed using
The size of a multi-dimensional array is fixed at the time it's created and cannot change during execution. Likewise, the several products used in the equation above will not change once the size of the array is set. This can be used to our advantage to reduce the number of multiplications
required to compute the element offsets. Instead of computing the products every time an element is accessed, we can compute and store the factor values and simply plug them into the equation when needed.