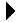6.2 Linear Search

The simplest solution to the sequence search problem is the sequential or linear search algorithm. This technique iterates over the sequence, one item at a time, until the specific item is found or all items have been examined. In Python, a target item can be found in a sequence using the in operator:

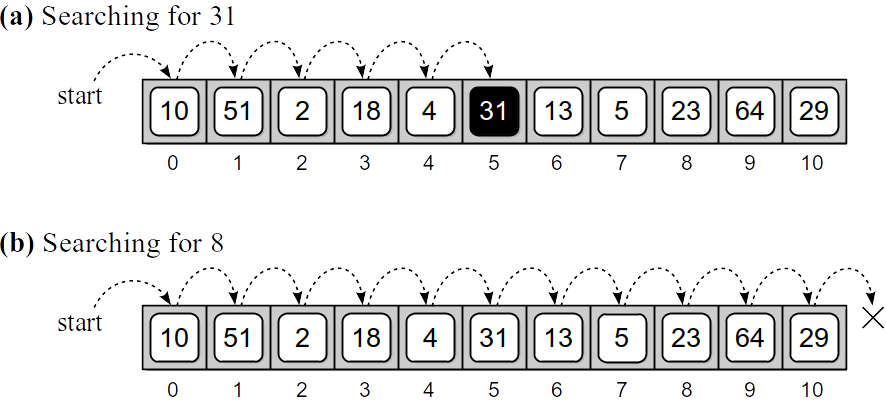
The use of the in operator makes our code simple and easy to read but it hides the inner workings. Underneath, the in operator is implemented as a linear search. Consider the unsorted 1-D array of integer values shown in Figure 6.2.1 (a). To determine if value 31 is in the array, the search begins with the value in the first element. Since the first element does not contain the target value, the next element in sequential order is compared to value 31. This process is repeated until the item is found in the sixth position. What if the item is not in the array? For example, suppose we want to search for value 8 in the sample array. The search begins at the first entry as before, but this time every item in the array is compared to the target value. It cannot be determined that the value is not in the sequence until the entire array has been traversed, as illustrated in Figure 6.2.1 (b).

Figure 6.2.1: Performing a linear search on an unsorted array: (a) the target item is found and (b) the item is not in the array.

Finding a Specific Item

The function in the source listing below implements the sequential search algorithm, which results in a boolean value indicating success or failure of the search.

This is the same operation performed by the Python in operator. A count-controlled loop is used to traverse through the sequence during which each element is compared against the target value. If the item is in the sequence, the loop is terminated and True is returned. Otherwise, a full traversal is performed and False is returned after the loop terminates.

linear search

worst-case: $\text{O}\left(n\right)$

To analyze the sequential search algorithm for the worst case, we must first determine what conditions constitute the worst case. Remember, the worst case occurs when the algorithm performs the maximum number of steps. For a sequential search, that occurs when the target item is not in the sequence and the loop iterates over the entire sequence. Assuming the sequence contains $n$ items, the linear search has a worst case time of $\text{O}\left(n\right)$.

Question 6.2.1

Does the linear search have a best case? If so, when does the best case occur? When does the worst case occur?

Yes.

• The best case occurs when the target is the first element in the sequence. In that case, the loop terminates after the first iteration.
• The worst case occurs when the target is not in the sequence. Thus, the loop iterates n times, or once for each element in the sequence.

Searching a Sorted Sequence

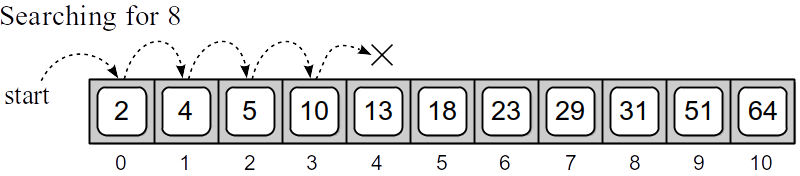
A linear search can also be performed on a sorted sequence, which is a sequence containing values in a specific order. For example, the values in the array illustrated in Figure 6.2.2 are in ascending or increasing numerical order. That is, each value in the array is larger than its predecessor.

Figure 6.2.2: The linear search on a sorted array.

A linear search on a sorted sequence works in the same fashion as that for the unsorted sequence, with one exception. It's possible to terminate the search early when the value is not in the sequence instead of always having to perform a complete traversal. For example, suppose we want to search for 8 in the array from Figure 6.2.2. When the fourth item, which is value 10, is examined, we know value 8 cannot be in the sorted sequence or it would come before 10. The implementation of a linear search on a sorted sequence is provided below.

The only modification to the earlier version is the inclusion of a test to determine if the current item within the sequence is larger than the target value. If a larger value is encountered, the loop terminates and False is returned. With the modification to the linear search algorithm, we have produced a better version, but the time-complexity remains the same. The reason is that the worst case occurs when the value is not in the sequence and is larger than the last element. In this case, we must still traverse the entire sequence of $n$ items.

Finding the Smallest Value

Instead of searching for a specific value in an unsorted sequence, suppose we wanted to search for the smallest value, which is equivalent to applying Python's min function to the sequence. A linear search is performed as before, but this time we must keep track of the smallest value found for each iteration through the loop, as illustrated in in the source listing below.

To prime the loop, we assume the first value in the sequence is the smallest and start the comparisons at the second item. Since the smallest value can occur anywhere in the sequence, we must always perform a complete traversal, resulting in a worst case time of $\text{O}\left(n\right)$.

Question 6.2.3

Does the findSmallest function have a best case? If so, when does it occur and what is the time-complexity in the best case?

Since the smallest value can occur anywhere within the sequence, we must always perform a complete traversal. Thus, searching for the smallest value within in a sequence does not have a best case.