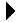6.8 Maintaining a Sorted List

The efficiency of some algorithms can be improved when working with sequences containing sorted values. We saw this earlier when performing a search using the binary search algorithm on a sorted sequence. Sorting algorithms can be used to create a sorted sequence, but they are typically applied to an unsorted sequence in which all of the values are known and the collection remains static. In other words, no new items will be added to the sequence nor will any be removed.

In some problems, like the set abstract data type, the collection does not remain static but changes as new items are added and existing ones are removed. If a sorting algorithm were applied to the underlying list each time a new value is added to the set, the result would be highly inefficient since even the best sorting algorithm requires $\text{O}\left(n\text{log}n\right)$ time. Instead, the sorted list can be maintained as the collection changes by inserting the new item into its proper position without having to re-sort the entire list. Note that while the sorting algorithms from the previous section all require $\text{O}\left(n^2\right)$ time in the worst case, there are more efficient sorting algorithms (which will be covered in Chapter 13) that only require $\text{O}\left(n\text{log}n\right)$ time.

To maintain a sorted list in real time, new items must be inserted into their proper position. The new items cannot simply be appended at the end of the list as they may be out of order. Instead, we must locate the proper position within the list and use the insert method to insert it into the indicated position. Consider the sorted list from Figure 6.3.1. If we want to add 25 to that list, then it must be inserted at position 7 following value 23.

To find the position of a new item within a sorted list, a modified version of the binary search algorithm can be used. The binary search uses a divide and conquer strategy to reduce the number of items that must be examined to find a target item or to determine the target is not in the list. Instead of returning True or False indicating the existence of a value, we can modify the algorithm to return the index position of the target if it's actually in the list or where the value should be placed if it were inserted into the list. The modified version of the binary search algorithm is shown below.

Note the change to the two return statements. If the target value is contained in the list, it will be found in the same fashion as was done in the original version of the algorithm. Instead of returning True, however, the new version returns its index position. When the target is not in the list, we need the algorithm to identify the position where it should be inserted.

Consider the illustration in Figure 6.8.1, which shows the changes to the three variables low, mid, and high as the binary search algorithm progresses in searching for value 25. The while loop terminates when either the low or high range variable crosses the other, resulting in the condition low > high. Upon termination of the loop, the low variable will contain the position where the new value should be placed. This index can then be supplied to the insert method to insert the new value into the list. The findOrderedPosition function can also be used with lists containing duplicate values, but there is no guarantee where the new value will be placed in relation to the other duplicate values beyond the proper ordering requirement that they be adjacent.

Figure 6.8.1: Performing a binary search on a sorted list when searching for value 25.