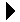8.1 The Queue ADT

A queue is a specialized list with a limited number of operations in which items can only be added to one end and removed from the other. A queue is also known as a first-in, first-out (FIFO) list. Consider Figure 8.1.1, which illustrates an abstract view of a queue. New items are inserted into a queue at the back while existing items are removed from the front. Even though the illustration shows the individual items, they cannot be accessed directly. The definition of the Queue ADT follows.

Figure 8.1.1: An abstract view of a queue containing five items.

The Queue ADT

A queue is a data structure that stores a linear collection of items in which access is restricted to a first-in first-out basis. New items are inserted at the back and existing items are removed from the front. The items are maintained in the order in which they are added to the structure.

Queue()

Creates a new empty queue, which is a queue containing no items.
isEmpty()

Returns a Boolean value indicating whether the queue is empty.
length()

Returns the number of items currently in the queue.
enqueue(item)

Adds the given item to the back of the queue.
dequeue()

Removes and returns the front item from the queue. An item cannot be dequeued from an empty queue.

Using the formal definition of the Queue ADT, we can now examine the code necessary to create the queue in Figure 8.1.1:

Q = Queue()

Q.enqueue(28)

Q.enqueue(19)

Q.enqueue(45)

Q.enqueue(13)

Q.enqueue(7)

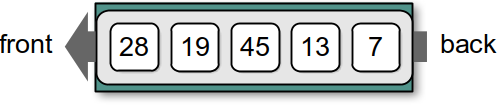
After creating a Queue object, we simply enqueue the five values in the order as they appear in the queue. We can then remove and use the values or add additional values to the queue. Figure 8.1.2 illustrates the result of performing several additional operations on the sample queue.

Figure 8.1.2: Abstract view of the queue after performing additional operations.

Chapter 8. Queues

8.2 Queue Implementation