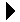4.8 Matrix Operations

A number of operations can be performed on matrices. We first describe some of the more common ones and provide examples as a review of matrix arithmetic.

Addition and Subtraction

Two $m\times n$ matrices can be added or subtracted to create a third $m\times n$ matrix. When adding two $m\times n$ matrices, corresponding elements are summed as illustrated here.

$$\left[\begin{array}{cl}0& 1\\ 2& 3\\ 4& 5\end{array}\right]+\left[\begin{array}{cc}6& 7\\ 8& 9\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}0+6& 1+7\\ 2+8& 3+9\\ 4+1& 5+0\end{array}\right]=\left[\begin{array}{cc}6& 8\\ 10& 12\\ 5& 5\end{array}\right]$$

Subtraction is performed in a similar fashion but the corresponding elements are subtracted instead of summed.

Multiplication

Matrix multiplication is only defined for matrices where the number of columns in the matrix on the lefthand side is equal to the number of rows in the matrix on the righthand side. The result is a new matrix that contains the same number of rows as the matrix on the lefthand side and the same number of columns as the matrix on the righthand side. In other words, given a matrix of size $m\times n$ multiplied by a matrix of size $n\times p$, the resulting matrix is of size $m\times p$.

In multiplying two matrices, each element of the new matrix is the result of summing the product of a row in the lefthand side matrix by a column in the righthand side matrix. In the example matrix multiplication illustrated here, the row and column used to compute entry (0,0) of the new matrix is shaded in light blue.

$$\begin{array}{cl}& \left[\begin{array}{cc}0& 1\\ 2& 3\\ 4& 5\end{array}\right]*\left[\begin{array}{ccc}6& 7& 8\\ 9& 1& 0\end{array}\right]\\ =& \left[\begin{array}{ccc}(0*6+1*9)& (0*7+1*1)& (0*8+1*0)\\ (2*6+3*9)& (2*7+3*1)& (2*8+3*0)\\ (4*6+5*9)& (4*7+5*1)& (4*8+5*0)\end{array}\right]\\ =& \left[\begin{array}{ccc}9& 1& 0\\ 39& 17& 16\\ 69& 33& 32\end{array}\right]\end{array}$$

Viewing matrix multiplication based on the element subscripts can help you to better understand the operation. Consider the two matrices from above and assume they are labeled A and B, respectively.

$$A=\left[\begin{array}{cc}{A}_{\mathrm{0,0}}& A_{\mathrm{0,1}}\\ A_{\mathrm{1,0}}& A_{\mathrm{1,1}}\\ A_{\mathrm{2,0}}& A_{\mathrm{2,1}}\end{array}\right]B=\left[\begin{array}{ccc}{B}_{\mathrm{0,0}}& B_{\mathrm{0,1}}& B_{\mathrm{0,2}}\\ B_{\mathrm{1,0}}& B_{\mathrm{1,1}}& B_{\mathrm{1,2}}\end{array}\right]$$

The computation of the individual elements resulting from multiplying A and B (C = A * B) is performed as follows:

$$\begin{array}{rcl}{C}_{\mathrm{0,0}}& =& A_{\mathrm{0,0}}*B_{\mathrm{0,0}}+A_{\mathrm{0,1}}*B_{\mathrm{1,0}}\\ C_{\mathrm{0,1}}& =& A_{\mathrm{0,0}}*B_{\mathrm{0,1}}+A_{\mathrm{0,1}}*B_{\mathrm{1,1}}\\ C_{\mathrm{0,2}}& =& A_{\mathrm{0,0}}*B_{\mathrm{0,2}}+A_{\mathrm{0,1}}*B_{\mathrm{1,2}}\\ C_{\mathrm{1,0}}& =& A_{\mathrm{1,0}}*B_{\mathrm{0,0}}+A_{\mathrm{1,1}}*B_{\mathrm{1,0}}\\ C_{\mathrm{1,1}}& =& A_{\mathrm{1,0}}*B_{\mathrm{0,1}}+A_{\mathrm{1,1}}*B_{\mathrm{1,1}}\\ C_{\mathrm{1,2}}& =& A_{\mathrm{1,0}}*B_{\mathrm{0,2}}+A_{\mathrm{1,1}}*B_{\mathrm{1,2}}\\ C_{\mathrm{2,0}}& =& A_{\mathrm{2,0}}*B_{\mathrm{0,0}}+A_{\mathrm{2,1}}*B_{\mathrm{1,0}}\\ C_{\mathrm{2,1}}& =& A_{\mathrm{2,0}}*B_{\mathrm{0,1}}+A_{\mathrm{2,1}}*B_{\mathrm{1,1}}\\ C_{\mathrm{2,2}}& =& A_{\mathrm{2,0}}*B_{\mathrm{0,2}}+A_{\mathrm{2,1}}*B_{\mathrm{1,2}}\end{array}$$

resulting in

$$\begin{array}{r}C=\left[\begin{array}{ccc}(A_{\mathrm{0,0}}*B_{\mathrm{0,0}}+A_{\mathrm{0,1}}*B_{\mathrm{1,0}})& (A_{\mathrm{0,0}}*B_{\mathrm{0,1}}+A_{\mathrm{0,1}}*B_{\mathrm{1,1}})& (A_{\mathrm{0,0}}*B_{\mathrm{0,2}}+A_{\mathrm{0,1}}*B_{\mathrm{1,2}})\\ (A_{\mathrm{1,0}}*B_{\mathrm{0,0}}+A_{\mathrm{1,1}}*B_{\mathrm{1,0}})& (A_{\mathrm{1,0}}*B_{\mathrm{0,1}}+A_{\mathrm{1,1}}*B_{\mathrm{1,1}})& (A_{\mathrm{1,0}}*B_{\mathrm{0,2}}+A_{\mathrm{1,1}}*B_{\mathrm{1,2}})\\ (A_{\mathrm{2,0}}*B_{\mathrm{0,0}}+A_{\mathrm{2,1}}*B_{\mathrm{1,0}})& (A_{\mathrm{2,0}}*B_{\mathrm{0,1}}+A_{\mathrm{2,1}}*B_{\mathrm{1,1}})& (A_{\mathrm{2,0}}*B_{\mathrm{0,2}}+A_{\mathrm{2,1}}*B_{\mathrm{1,2}})\end{array}\right]\end{array}$$

Scaling

A matrix can be uniformly scaled, which modifies each element of the matrix by the same scale factor. A scale factor of less than 1 has the effect of reducing the value of each element whereas a scale factor greater than 1 increases the value of each element. Scaling a matrix by a scale factor of 3 is illustrated here:

$$3\left[\begin{array}{cc}6& 7\\ 8& 9\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}3*6& 3*7\\ 3*8& 3*9\\ 3*1& 3*0\end{array}\right]=\left[\begin{array}{cc}18& 21\\ 24& 27\\ 3& 0\end{array}\right]$$

Transpose

Another useful operation that can be applied to a matrix is the matrix transpose. Given a $m\times n$ matrix, a transpose swaps the rows and columns to create a new matrix of size $n\times m$ as illustrated here:

$${\left[\begin{array}{cc}0& 1\\ 2& 3\\ 4& 5\end{array}\right]}^T=\left[\begin{array}{ccc}0& 2& 4\\ 1& 3& 5\end{array}\right]$$