7.10 The Sparse Matrix Revisited

On this page...

An Array of Linked Lists Implementation
Comparing the Implementations

In Chapter 5, we defined and implemented the Sparse Matrix ADT. Remember, a sparse matrix is a matrix containing a large number of zero elements as illustrated by the sample matrix below.

$[\begin{array}{cccccccc} \cdot & 3 & \cdot & \cdot & 8 & \cdot & \cdot & \cdot \\ 2 & \cdot & \cdot & 1 & \cdot & \cdot & 5 & \cdot \\ \cdot & \cdot & 9 & \cdot & \cdot & 2 & \cdot & \cdot \\ \cdot & 7 & \cdot & \cdot & \cdot & \cdot & \cdot & 3 \\ \cdot & \cdot & \cdot & \cdot & 4 & \cdot & \cdot & \cdot \end{array}]$

Instead of providing space for every element in the matrix, we need only store the non-zero elements. In our original implementation, we used a list to store the non-zero elements of the matrix, which were stored as MatrixElement objects. This improved the time-complexity of many of the matrix operations when compared to the use of a 2-D array.

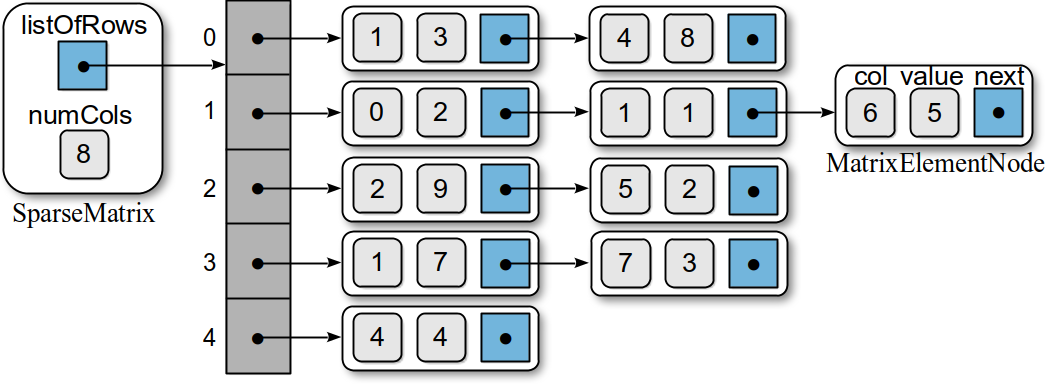
We can further improve the Sparse Matrix ADT by using the linked list structure. Instead of storing the elements in a single list, however, we can use an array of sorted linked lists, one for each row of the matrix. The non-zero elements for a given row will be stored in the corresponding linked list sorted by column index. The row index is not needed since it corresponds to a specific linked list within the array of linked lists. The sparse matrix from above is illustrated in Figure 7.10.1 stored using an array of linked lists.

Figure 7.10.1: A sparse matrix implemented as an array of sorted linked lists.

An Array of Linked Lists Implementation

To implement the Sparse Matrix ADT using an array of sorted linked lists, we create a new Sparse Matrix class, as shown in in the listing below.

Program Listing

Program: sparse_class.py

# Implementation of the Sparse Matrix ADT using an array of linked lists.
from ezarrays import Array
class SparseMatrix :
# Creates a sparse matrix of size numRows x numCols initialized to 0.
def __init__(self, numRows, numCols) :
self._numCols = numCols
self._listOfRows = Array(numRows)
# Returns the number of rows in the matrix.
def numRows(self) :
return len(self._listOfRows)
# Returns the number of columns in the matrix.
def numCols(self) :
return self._numCols
# Returns the value of element (i,j): x[i,j]
def __getitem__(self, ndxTuple) :
......
# Sets the value of element (i,j) to the value s: x[i,j] = s
def __setitem__(self, ndxTuple, value) :
(row, col) = ndxTuple
predNode = None
curNode = self._listOfRows[row]
while curNode and curNode.col != col :
predNode = curNode
curNode = curNode.next
# See if the element is in the list.
if curNode and curNode.col == col :
if value == 0.0 : # remove the node.
if curNode == self._listOfRows[row] :
self._listOfRows[row] = curNode.next
else :
predNode.next = curNode.next
else : # change the node's value.
curNode.value = value
# Otherwise, the element is not in the list.
elif value != 0.0 :
newNode = MatrixElementNode( col, value )
newNode.next == curNode
if curNode == self._listOfRows[row] :
self._listOfRows[row] = newNode
else :
predNode.next = newnode
# Scales the matrix by the given scalar.
def scaleBy(self, scalar) :
for row in range(self.numRows()) :
curNode = self._listOfRows[row]
while curNode :
curNode.value *= scalar
curNode = curNode.next
# Creates and returns a new matrix that is the transpose of this matrix.
def transpose(self):
......
# Matrix addition: newMatrix = self + rhsMatrix.
def __add__(self, rhsMartrix) :
# Make sure the two matrices have the correct size.
assert (rhsMatrix.numRows() == self.numRows() and
rhsMatrix.numCols() == self.numCols()),
"Matrix sizes not compatable for adding."
# Create a new sparse matrix of the same size.
newMatrix = SparseMatrix(self.numRows(), self.numCols())
# Add the elements of this matrix to the new matrix.
for row in range(self.numRows()) :
curNode = self._listOfRows[row]
while curNode :
newMatrix[row, curNode.col] = curNode.value
curNode = curNode.next
# Add the elements of the rhsMatrix to the new matrix.
for row in range(rhsMatrix.numRows()) :
curNode = rhsMatrix._listOfRows[row]
while curNode :
value = newMatrix[row, curNode.col]
value += curNode.value
newMatrix[row, curNode.col] = value
curNode = curNode.next
# Return the new matrix.
return newMatrix
# --- Matrix subtraction and multiplication ---
# def __sub__( self, rhsMatrix ) :
# def __mul__( self, rhsMatrix ) :
# Storage class for creating matrix element nodes.
class MatrixElementNode :
def __init__(self, col, value) :
self.col = col
self.value = value
self.next = None

In the constructor, two class fields are created: one to store the number of columns in the matrix and another to store the array of head references to the linked lists in which the matrix elements will be stored. An array is created whose size is equal to the number of rows in the matrix. The individual elements are initialized to None to represent empty linked lists since there are no non-zero elements in the sparse matrix initially. Note we did not provide a field to store the number of rows as that information can be obtained from the length of the array. Thus, numRows simply calls the array's length operation.

The MatrixElementNode class, provided in lines 95 -99, is a modified version of the MatrixElement class used in Chapter 5. The row component has been removed while the next link field was added in order to use the objects as linked nodes. When elements are added to the sparse matrix, nodes will be added to the individual linked lists based on the row index of the element. Thus, the row component does not have to be stored in each node.

Changing Element Values

The __setitem__ method is the main linked list management routine for the underlying structure. This method not only provides for the modification of element values, but it also handles node insertions for new non-zero elements and node removals when an element becomes zero. The three operations handled by this method can be combined to produce an efficient implementation.

The first step is to position the two external reference variables predNode and curNode along the linked list corresponding to the indicated row index. While only the curNode reference will be needed for a simple element value modification, predNode will be needed if we have to insert a new node or remove an existing node. After positioning the two references, we can then determine what action must be taken. If the element corresponding to the given row and col indices is in the linked list, curNode will be pointing to a node and the col field of that node will be that of the element. In this case, either the value stored in the node is changed to the new non-zero value or the node has to be deleted when the new value is zero. Modifying the value only requires changing the value field of the curNode. Removing the element entry for a zero value is also straightforward since the two external references have been positioned correctly and the links can be changed as outlined in Section 7.5.

If the element is not represented by a node in the linked list of the corresponding row and the new value is non-zero, then a new node must be inserted in the proper position based on the predNode and curNode references. The only difference in the insertion operation from that used earlier in the chapter is that the head reference is stored in one of the elements of the _listOfRows array instead of its own variable. If the element is already a zero-entry and the new value is zero, no action is required.

Setting the value of a matrix element requires ${Olinear $} time in the worst case, where $n$ is the number of columns in the matrix. This value is obtained by observing that the most time-consuming part is the positioning of the two references, curNode and predNode, which require a complete list traversal in the worst case. Since a linked list contains a single row, we know it will contain at most $n$ nodes.

Matrix Scaling

The scaleBy method is very similar to the version used in the list implementation of the original Sparse Matrix ADT from Chapter 5. We need only traverse over each of the individual linked lists stored in the _listOfRows array, during which we scale the value stored in each node. Remember, this is sufficient as elements not represented by nodes in the linked lists have zero values and thus would not be affected by a scaling factor. The matrix scaling operation requires $O (k)$ time in the worst case since only the $k$ non-zero elements are stored in the structure.

Matrix Addition

The __add__ method for this version of the sparse matrix, which is provided in lines 62 - 88, also follows the four steps outlined in Section 5.10. We first create a new SparseMatrix object that will contain the new matrix resulting from the addition. Then, the contents of the self or lefthand-side matrix is copied to the new matrix, one element at a time. Finally, we traverse over the non-zero elements of the righthand-side matrix and add the values of its non-zero elements to the new matrix.

This implementation of the addition operation, which requires $O (k n)$ time in the worst case, is not the most efficient. Instead of using the __getitem__ and __setitem__ operations, we can use temporary traversal reference variables with each matrix to directly access the non-zero values in the two source matrices and to store the resulting non-zero values in the new matrix. A new implementation can be devised that only requires $O (k)$ time in the worst case.

Comparing the Implementations

The Sparse Matrix ADT implemented as an array of linked lists can be evaluated for any of the three cases: best, average, and worst. The analysis, which is left as an exercise, depends on the relationship between the total number of non-zero elements, $k$ , and the number of columns, $n$ , in the matrix.

We implemented the Matrix ADT using a 2-D array, which can also be used to store a sparse matrix and we implemented the Sparse Matrix ADT using two different data structures: a list of MatrixElement objects, and an array of linked lists. Table 7.10.1 provides a comparison of the worst case time-complexities between the three implementations for several of the matrix operations. The 2-D array implementation offers the best advantage of quick element access with the __getitem__ and __setitem__ methods, but the other matrix operations are more costly. While both the Python list and the array of linked lists implementations provide similar times, the array of linked lists version will typically provide better times since the efficiency for many of the operations is based on the number of columns in the matrix and not the total number of non-zero elements.

Matrix Operation	2-D Array	Python List	Linked Lists
`s = SparseMatrix()`	$O (1)$	$O (1)$	$O (1)$
`s.numRows()`	$O (1)$	$O (1)$	$O (1)$
`s.numCols()`	$O (1)$	$O (1)$	$O (1)$
`x = s[i,j]`	$O (1)$	$O (k)$	$O (n)$
`s[i,j] = x`	$O (1)$	$O (k)$	$O (n)$
`s.scaleBy(x)`	$O (n^{2})$	$O (k)$	$O (k)$
`r = s + t`	$O (n^{2})$	$O (k^{2})$	$O (k n)$

Table 7.10.1: Comparison of the Matrix and Sparse Matrix ADT implementations.

7.9 The Sorted Linked List

Chapter 7. Linked Structures

7.11 Application: Polynomials