5.8 Implementing the Set

On this page...

The Constructor
Set Contents
Adding Elements
Removing Elements
Comparing Two Sets
The Set Union
Program Listing

To implement the Set ADT, we must select a data structure based on the same criteria we used for the Bag ADT from Section 2.2. Since we are trying to replicate the functionality of the set structure provided by Python, we don't want to use that structure. That leaves the array, list, and map containers for consideration in implementing the Set ADT.

The storage requirements for the bag and set are very similar with the difference being that a set cannot contain duplicates. The map would seem to be the ideal choice since it can store unique items, but it would waste space in this case. Remember, the dictionary stores key/value pairs, which requires two data fields per entry. We could store the individual items of the set in the key fields and leave the value fields empty, but that would use twice the amount of storage than necessary. This waste does not occur with an array or list.

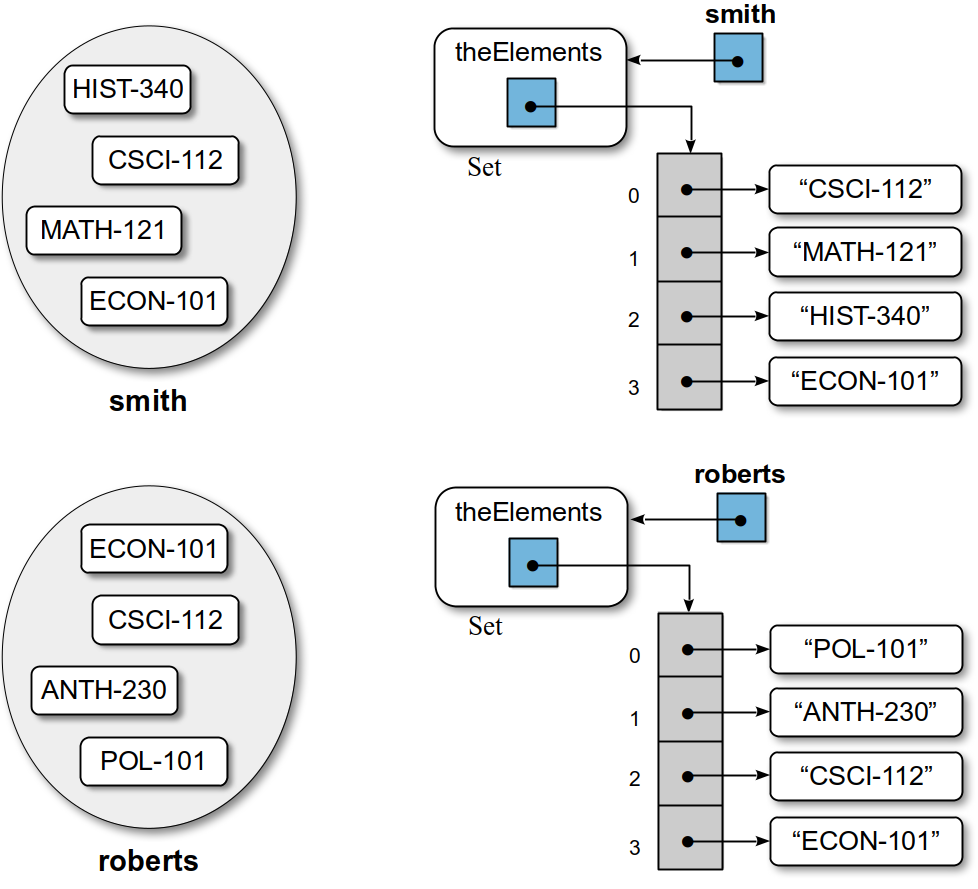
An array could be used to implement the set, but a set can contain any number of elements and by definition an array has a fixed size. To use the array structure, we would have to manage the expansion of the array when necessary in the same fashion as is done for the list. Since the list can grow as needed, it seems ideal for storing the elements of a set just as it was for the bag and it does provide for the complete functionality of the ADT. Since the list allows for duplicate values, however, we must make sure as part of the implementation that no duplicates are added to our set. Sample instances for two sets representing the course schedules for two students is illustrated in Figure 5.8.1.

Figure 5.8.1: Two instances of the Set class implemented as a list: abstract view (left) and physical view (right).

The Constructor

The definition of the class constructor for the Set ADT specifies the creation of an empty set. Thus, we must decide how to represent an empty set using the vector. The easiest approach is to represent an empty set with an empty vector as we did for the Bag class.

class Set :  

  def __init__(self) :

    self._theElements = list()

The isEmpty method can then be implemented to check for a vector of length 0:

def isEmpty(self) :

  return len(self._theElements) == 0

Set Contents

As with the Bag class, the length of the set is simply the number of elements in the underlying list:

def __len__(self) :

  return len(self._theElements)

The definition of the Set ADT explicitly indicates that the elements added to the set must be comparable. That is, we must be able to use any of Python's relational operators to compare two elements in the set. Since the elements must be comparable, we can use the in operator on the underlying list to implement the contains operation for the Set ADT:

def __contains__(self, element) :

  return element in self._theElements   

Adding Elements

As indicated earlier, we must ensure that duplicate values are not added to set since the list structure does not handle this for us. When implementing the add method, we must first determine if the supplied element is already in the list or not:

def add(self, element) :                   

  if element not in self :

    self._theElements.append( element )     

If the element is not a duplicate, we can simply append the value to the end of the list; if the element is a duplicate, we do nothing. The reason for this is that the definition of the add operation indicates no action is taken when an attempt is made to add a duplicate value. This is known as a no op, which is short for no operation and indicates no action is taken. No ops are appropriate in some cases, which will be stated implicitly in the definition of an abstract data type by indicating no action is to be taken when the precondition fails as we did with the add operation.

Removing Elements

The definition of the remove operation is explicit in its requirement that an element must be in the set before attempting to remove it. We must check this precondition before using the remove operation of the underlying list structure to remove the element:

def remove(self, element) :

  assert element in self, "The element must be in the set."

  self._theElements.remove( item )

The implementation of the clear operation is left as an exercise.

Comparing Two Sets

For the operations that require a second set as an argument, we can use the operations of the Set ADT itself to access and manipulate the data of the second set. Consider the subset operation. To determine if one set is the subset of another, we can iterate over the list of elements in the self set and make sure each is contained in setB. If just one element in the self set is not in setB, then it is not a subset. The implementation of the isSubsetOf method follows:

def isSubsetOf(self, setB) :               

  for element in self._theElements :

    if element not in setB :

      return False

  return True

To determine if two sets contain the exact same elements, we first check to make sure the two sets contain the same number of elements; otherwise, by definition they cannot be equal. It would be inefficient to compare the individual elements since we already know the two sets cannot be equal. After verifying the size of the lists, we can test to see if the self set is a subset of setB by calling the isSubsetOf method on the self set. This is a valid test since two equal sets are subsets of each other and we already know they are of the same size. The implementation of the set equals operation follows:

def __eq__(self, setB) :                   

  if len(self) != len(setB) :

    return False

  else :

    return self.isSubsetOf(setB)

PROGRAMMING TIP
	Avoid Reinventing the Wheel Using operations provided by a class to implement other methods of that same class allows you to take advantage of the abstraction and avoid "reinventing the wheel" by duplicating code in several places.

The Set Union

Some of the operations create and return a new set based on the original, but the original is not modified. This is accomplished by creating a new set and populating it with the appropriate data from the other sets. Consider the union method, which creates a new set from the self set and setB passed as an argument to the method.

def union(self, setB) :                    

  newSet = Set()  

  newSet._theElements.extend(self._theElements)

  for element in setB._theElements :

    if element not in self :

      newSet._theElements.append(element)

  return newSet

Creating a new set, populated with the unique elements of the other two sets, requires three steps:

create a new set
fill the newSet with the elements from setB, and
iterate through the elements of the self set, during which each element is added to the newSet if that element is not in setB.

For the first step, we simply create a new instance of the Set class. The second step is accomplished with the use of the list extend method. It directly copies the entire contents of the list used to store the elements of the self set to the list used to store the elements of the newSet. For the final step, we iterate through the elements of setB and add those elements to the the newSet that are not in the self set.

The unique elements are added to the newSet by appending them to the list used to store the elements of the newSet. The intersect and difference operations can be implemented in a similar fashion and are left as exercises.

Program Listing

The implementation of the Set ADT using a Python list to store and manage the elements is provided in the listing below

Program Listing

Program: linearset.py

# Implementation of the Set ADT container using a Python list.
class Set :
# Creates an empty set instance.
def __init__(self) :
self._theElements = list()
# Returns the number of items in the set.
def __len__(self) :
return len(self._theElements)
# Returns True if the set is empty and False otherwise.
def isEmpty(self) :
return len(self._theElements) == 0
# Determines if an element is in the set.
def __contains__(self, element) :
return element in self._theElements
# Adds a new unique element to the set.
def add(self, element) :
if element not in self :
self._theElements.append( element )
# Removes an element from the set.
def remove(self, element) :
assert element in self, "The element must be in the set."
self._theElements.remove( item )
# Removes all of the elements from the set.
def clear(self) :
......
# Determines if two sets are equal.
def __eq__(self, setB) :
if len(self) != len(setB) :
return False
else :
return self.isSubsetOf(setB)
# Determines if this set is a subset of setB.
def isSubsetOf(self, setB) :
for element in self._theElements :
if element not in setB :
return False
return True
# Creates a new set from the union of this set and setB.
def union(self, setB) :
newSet = Set()
newSet._theElements.extend(self._theElements)
for element in setB._theElements :
if element not in self :
newSet._theElements.append(element)
return newSet
# Creates a new set from the intersection: self set and setB.
def interset( self, setB ):
......
# Creates a new set from the difference: self set and setB.
def difference( self, setB ):
......
# Returns an iterator for traversing the list of items.
def __iter__( self ):
return iter(self._theElements)

5.7 Set Operations

Chapter 5. Algorithm Analysis

5.9 Evaluating the Set Implementation