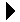5.10 Application: The Sparse Matrix

On this page...

List-Based Implementation
Efficiency Analysis

A matrix containing a large number of zero elements is called a sparse matrix. Sparse matrices are very common in scientific applications, especially those dealing with systems of linear equations. A sparse matrix is formally defined to be an $m n$ matrix that contains $k$ non-zero elements such that $k ≪ m � n$ . The 2-D array data structure used to implement the Matrix ADT in Chapter 4 works well for general matrices. But when used to store huge sparse matrices, large amounts of memory can be wasted and the operations can be inefficient since the zero elements are also stored in the 2-D array.

Consider the sample $5 8$ sparse matrix in Figure 5.10.1. Is there a different structure or organization we can use to store the elements of a sparse matrix that does not waste space? One approach is to organize and store the non-zero elements of the matrix within a single list instead of a 2-D array.

[\begin{array}{cccccccc} \cdot & 3 & \cdot & \cdot & 8 & \cdot & \cdot & \cdot \\ 2 & \cdot & \cdot & 1 & \cdot & \cdot & 5 & \cdot \\ \cdot & \cdot & 9 & \cdot & \cdot & 2 & \cdot & \cdot \\ \cdot & 7 & \cdot & \cdot & \cdot & \cdot & \cdot & 3 \\ \cdot & \cdot & \cdot & \cdot & 4 & \cdot & \cdot & \cdot \end{array}]

Figure 5.10.1: A sample sparse matrix with zero elements indicated with dots.

List-Based Implementation

In this section, we define and implement a class for storing and working with sparse matrices in which the non-zero elements are stored in a list. The operations of a sparse matrix are the same as those for a general matrix and many of them can be implemented in a similar fashion as was done for the Matrix class in Section 4.9. This would be sufficient if our only objective was to reduce the storage cost, but we can take advantage of only storing the non-zero elements to improve the efficiency of several of the sparse matrix operations. The implementation of the SparseMatrix class is provided in source listing below.

Program Listing

Program: sparsematrix.py

# Implementation of the Sparse Matrix ADT using a list.
class SparseMatrix :
# Create a sparse matrix of size numRows x numCols initialized to 0.
def __init__( self, numRows, numCols ):
self._numRows = numRows
self._numCols = numCols
self._elementList = list()
# Return the number of rows in the matrix.
def numRows( self ):
return self._numRows
# Return the number of columns in the matrix.
def numCols( self ):
return self._numCols
# Return the value of element (i, j): x[i,j]
def __getitem__( self, ndxTuple ):
......
# Set the value of element (i,j) to the value s: x[i,j] = s
def __setitem__( self, ndxTuple, scalar ):
assert len(ndxTuple) == 2, "Invalid number of element subscripts."
assert (row >= 0 and row < self._numRows and
col >= 0 and col < self._numCols), "Array subscript out of range."
ndx = self._findPosition( ndxTuple[0], ndxTuple[1] )
if ndx >= 0 : # if the element is found in the list.
if scalar != 0.0 :
self._elementList[ndx].value = scalar
else :
self._elementList.pop( ndx )
else : # if the element is zero and not in the list.
if scalar != 0.0 :
element = MatrixElement( ndxTuple[0], ndxTuple[1], scalar )
self._elementList.append( element )
# Scale the matrix by the given scalar.
def scaleBy( self, scalar ):
for element in self._elementList :
element.value *= scalar
# The additional methods should be placed here.....
# def __add__( self, rhsMatrix ):
# def __sub__( self, rhsMatrix ):
# def __mul__( self, rhsMatrix ):
# def transpose( self ):
# Helper method used to find a specific matrix element (row,col) in the
# list of non-zero entries. None is returned if the element is not found.
def _findPosition( self, row, col ):
n = len( self._elementList )
for i in range( n ) :
if row == self._elementList[i].row and \
col == self._elementList[i].col:
return i # return the index of the element if found.
return -1 # return -1 when the element is zero.
# Storage class for holding the non-zero matrix elements.
class MatrixElement:
def __init__( self, row, col, value ):
self.row = row
self.col = col
self.value = value

Note the use of the new class name to distinguish this version from the original Matrix ADT and to indicate it is meant for use with sparse matrices. A sample instance of the class that corresponds to the sparse matrix from Figure 5.10.1 is illustrated in Figure 5.10.2.

Attach:Chapter5.ApplicationSparseMatrix/sparselist.png Δ

Figure 5.10.2: A list of MatrixElement objects representing a sparse matrix.

Constructor

The constructor defines three attributes for storing the data related to the sparse matrix. The _elementList field stores MatrixElement objects representing the non-zero elements. Instances of the storage class contain not only the value for a specific element but also the row and column indices indicating its location within the matrix. The _numRows and _numCols fields are used to store the dimensions of the matrix. This information cannot be obtained from the element list as was done with the Array 2 D used in the implementation of the Matrix ADT in Chapter 4.

Helper Method

Since the element list only contains the non-zero entries, accessing an individual element is no longer as simple as directly referencing an element of the rectangular grid. Instead, we must search through the list to locate a specific non-zero element. The helper method _findPosition performs this linear search by iterating through the element list looking for an entry with the given row and column indices. If found, it returns the list index of the cell containing the element; otherwise, -1 is returned to indicate the absence of the element.

Modifying an Element

The __setitem__ method for the SparseMatrix class is a bit more involved than that for the Matrix class. The value of an element cannot be directly set as was done when using the 2-D array. Instead, there are four possible conditions:

The element is in the list (and thus non-zero) and the new value is non-zero.
The element is in the list, but the new value is zero, turning the element into a zero element.
The element is not currently in the list and the new value is non-zero.
The element is not currently in the list, and the new value is zero.

The fist step in implementing the __setitem__ method, as shown in lines 23 - 33 of the class implementation, is to determine if the element is in the list using the _findPosition helper method. If the entry is in the list, we either change the corresponding element to the new value if it is non-zero or we remove the entry from the list when the new value is zero. On the other hand, if there is no entry for the given element, then a new MatrixElement object must be created and appended to the list. Of course, this is only done if the new value is non-zero.

Matrix Scaling

Scaling a matrix requires multiplying each element of the matrix by a given scale factor. Since the zero elements of the matrix are not affected by the scale factor, the implementation of this operation for the sparse matrix is as simple as traversing the list of MatrixElement objects and scaling the corresponding value.

Matrix Addition

In the add method of the Matrix class implemented in Chapter 4, we iterated over the 2-D array and added the values, element by element, and stored the results in the corresponding element of the new matrix. We could use the same loop structure shown here for the SparseMatrix class:

 # Add the corresponding elements in the two matrices.

for r in range(self.numRows()) :

  for c in range(self.numCols()) :

    newMatrix[ r, c ] = self[ r, c ] + rhsMatrix[ r, c ]

return newMatrix

Given a matrix of size $n n$ , this implementation of the add operation requires $O (n^{2})$ time. If the sparse matrix contains a significant number of zero elements, this can be inefficient. Instead, only the non-zero elements contained in the two sparse matrices must be considered when adding to matrices. The nested loops can be replaced with two separate loops to reduce the number of required iterations. The new solution for sparse matrix addition requires four steps:

Verify the size of the two matrices to ensure they are the same as required by matrix addition.
Create a new SparseMatrix object with the same number of rows and
columns as the other two.
Duplicate the elements of the self matrix and store them in the new matrix.
Iterate over the element list of the right-hand side matrix (rhsMatrix) to add the non-zero values to the corresponding elements in the new matrix.

The implementation of the add operation is provided below

Program Listing

Program: add2.py

class SparseMatrix :
# ...
def __add__( self, rhsMatrix ):
assert rhsMatrix.numRows() == self.numRows() and \
rhsMatrix.numCols() == self.numCols(), \
"Matrix sizes not compatible for the add operation."
# Create the new matrix.
newMatrix = SparseMatrix( self.numRows(), self.numCols() )
# Duplicate the lhs matrix. The elements are mutable, thus we must
# create new objects and not simply copy the references.
for element in self._elementList :
dupElement = _MatrixElement(element.row, element.col, element.value)
newMatrix._elementList.append( dupElement )
# Iterate through each non-zero element of the rhsMatrix.
for element in rhsMatrix._elementList :
# Get the value of the corresponding element in the new matrix.
value = newMatrix[ element.row, element.col ]
value += element.value
# Store the new value back to the new matrix.
newMatrix[ element.row, element.col ] = value
# Return the new matrix.
return newMatrix

The first two steps of the add operation are straightforward. The third step of copying the elements of the self matrix to the new matrix requires a list duplication, which is handled by the first loop. The second loop handles the fourth step outlined above by iterating over the list of MatrixElement objects in the rhsMatrix and adding their values to the corresponding values in the new sparse matrix. Note the use of the __getitem__ and __setitem__ methods in the second loop. This is necessary since the two methods properly manage any zero elements that may currently exist in the newMatrix or that may result after adding corresponding elements.

Efficiency Analysis

To evaluate the various operations of the sparse matrix, we can assume a square $n n$ matrix since this would be the worst possible case. We begin with the _findPosition helper method, which performs a sequential search over the list of non-zero entries. The worst case occurs when every item in the list is examined. But how many iterations does that require? It depends on the size of the element list. From the definition of a sparse matrix, we know it contains $k$ non-zero elements such that $k ≪ n^{2}$ . Thus, the worst case run time of the helper method is $O (k)$ .

The __setitem__ method calls _findPosition, which requires $k$ time. It then changes the value of the target entry, which is a constant time operation, or either removes an entry from the list or appends a new entry. The list operations require $k$ time in the worst case, resulting in an overall time of $O (k)$ for the set operation. The __getitem__ method can be evaluated in the same fashion and also has a worst case time of $O (k)$ .

To evaluate the operations that manipulate two SparseMatrix objects, we can specify that both matrices are of the same size or that $k$ will represent the size of the larger of the two lists. Computing the worst case time for the new add method requires that we first determine the complexity of the individual steps.

The size verification and new matrix creation are constant steps.
To duplicate the entries of the lefthand side sparse matrix requires $k$ time since append has an amortized cost of $O (1)$ .
The second loop iterates over the element list of the righthand side matrix, which we have assumed also contains $k$ elements. Since the get and set element operations used within the loop each require $k$ time in the worst case, the loop requires $2 k * k$ or $2 k^{2}$ time.

Combining this with the time for the previous steps, the add operation is $O (k^{2})$ in the worst case. Is this time better than that for the add operation from the Matrix class implemented as a 2-D array? That depends on the size of $k$ . If there were no zero elements in either matrix, then $k = n^{2}$ , which results in a worst case time of $O (n^{4})$ . Remember, however, this implementation is meant to be used with a sparse matrix in which $k ≪ m � n$ . In addition, the add operation only depends on the size of the element list, $k$ . Increasing the value of $m$ or $n$ does not increase the size of $k$ . For the analysis of this algorithm, $m$ and $n$ simply provide a maximum value for $k$ and are not variables in the equation.

The use of a list as the underlying data structure to store the non-zero elements of a sparse matrix is a much better implementation than the use of a 2-D array as it can save significant storage space for large matrices. On the other hand, it introduces element access operations that are more inefficient than when using the 2-D array. Table 5.10.1 provides a comparison of the worst case time-complexities for several of the operations of the Matrix class using a 2-D array and the SparseMatrix class using a list. In later chapters, we will further explore the Sparse Matrix ADT and attempt to improve the time-complexities of the various operations.

Operation	Matrix	Sparse Matrix
`s = SparseMatrix()`	$O (n^{2})$	$O (1)$
`s.numRows()`	$O (1)$	$O (1)$
`s.numCols()`	$O (1)$	$O (1)$
`s.scaleBy(x)`	$O (n^{2})$	$O (k)$
`x = s[i, j]`	$O (1)$	$O (k)$
`s[i, j] = x`	$O (1)$	$O (k)$
`r = s + t`	$O (n^{2})$	$O (k^{2})$

Table 5.10.1: Comparison of the worst case time-complexities for the Matrix class implemented using a 2-D array and the SparseMatrix class using a list.

5.9 Evaluating the Set Implementation

Chapter 5. Algorithm Analysis

Chapter Exercises