To implement the MultiArray ADT, the elements of the multi-dimensional array
can be stored in a single 1-D array in row-major order. Not only does this create a fast and compact array structure, but it's also the actual technique used by most programming languages.
Constructor
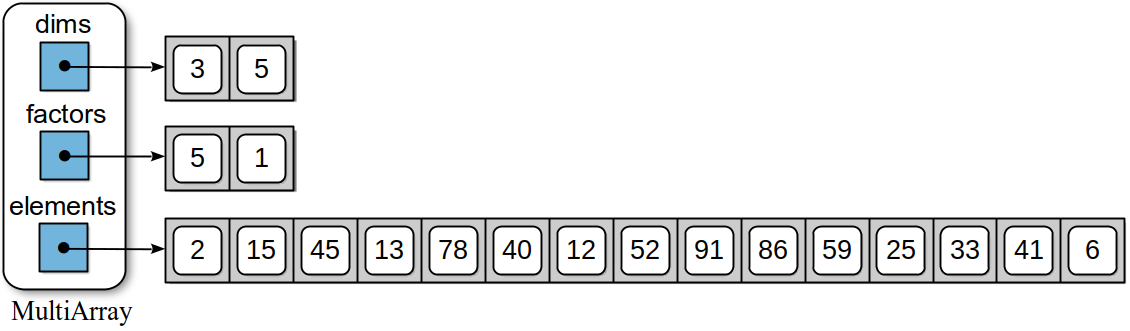
The constructor will require three data fields: _dims stores the sizes of the individual dimensions; _factors stores the factor values used in the index equation; and _elements is used to store the 1-D array used as the physical storage for the multi-dimensional array. A sample instance of the MultiArray class is illustrated in Figure 4.6.1.
Figure 4.6.1: A sample
MultiArray object for the 2-D array from
Figure 4.5.1
Variable Length Arguments |
The definition of the MultiArray ADT requires a variable-length argument for the constructor and the two element access methods. The number of arguments passed to each method is supposed to equal the number of dimensions in the array. Python functions and methods can be defined to accept a variable number of arguments, which is exactly what we need to implement the MultiArray ADT. Consider the following function, which accepts any number of arguments (assumed to be numerical in this example) and then prints how many arguments were passed and the sum of those arguments:
def func( *args ):
print "Number of arguments: ", len( args )
sum = 0
for value in args :
sum += value
print( "Sum of the arguments: ", sum )
When using the function, we can pass a variable number of arguments for each invocation. For example, all of the following are valid function calls:
func( 12 )
func( 5, 8, 2 )
func( 18, -2, 50, 21, 6 )
which results in the following output:
Number of arguments: 1
Sum of the arguments: 12
Number of arguments: 3
Sum of the arguments: 15
Number of arguments: 5
Sum of the arguments: 93
The asterisk next to the argument name (*args) tells Python to accept any number of arguments and to combine them into a tuple. The tuple is then passed to the function and assigned to the formal argument marked with the asterisk. Note the asterisk is only used in the argument list to indicate that the function or~method can accept any number of arguments. It is not part of the argument name. The len function can be applied to the tuple to determine the number of actual arguments passed to the function. The individual arguments, which are elements in the tuple, can be accessed by using the subscript notation or by iterating the collection.
|
The constructor is defined to accept a variable length argument as required in the ADT definition. The resulting tuple will contain the sizes of the individual dimensions and is assigned to the _dims field. The dimensionality of the array must be verified at the beginning of the constructor as the MultiArray ADT is meant for use with arrays of two dimensions or more.
assert len(dimensions) > 1, "The array must have 2 or more dimensions."
self._dims = dimensions
The elements of the multi-dimensional array will be stored in a 1-D array. The fixed size of the array can be computed as the product of the dimension lengths by traversing over the tuple containing the variable-length argument. During the traversal, the precondition requiring all dimension lengths be greater than zero is also evaluated. The 1-D array is created using the Array class defined earlier in the chapter.
size = 1
for d in dimensions :
assert d > 0, "Dimensions must be > 0."
size *= d
self._elements = Array(size)
Finally, a 1-D array is created and assigned to the _factors field. The size of the array is equal to the number of dimensions in the multi-dimensional array. This array will be initialized to the factor values used in Equation 4.4 for computing the element offsets. The actual computation and initialization is performed by the _computeFactors helper method, which is left as an exercise.
self._factors = Array(len(dimensions))
self._computeFactors()
The complete constructor is shown below:
class MultiArray :
def __init__(self, *dimensions) :
assert len(dimensions) > 1, \
"The array must have 2 or more dimensions."
self._dims = dimensions
size = 1
for d in dimensions :
assert d > 0, "Dimensions must be > 0."
size *= d
self._elements = Array(size)
self._factors = Array(len(dimensions))
self._computeFactors()
Dimensionality and Lengths
In the multi-dimensional version of the array, there is no single length value. Instead, each dimension of the array has an associated size. Python's len function cannot be used for this task since we must specify a particular dimension to obtain its size. Instead, the length method, is used:
def length(self, dim) :
assert dim >= 1 and dim < len(self._dims), "Dimension component out of range."
return self._dims[dim - 1]
The method first verifies the given dimension index is between and , which is the legal range specified in the ADT definition. The size of the requested dimension is then returned using the appropriate value from the _dims tuple.
The numDims method returns the dimensionality of the array, which can be obtained from the number of elements in the _dims tuple
def numDims(self) :
return len(self._dims)
Element Access
Access to individual elements within an -D array requires an -tuple or multi-component subscript, one for each dimension. As indicated in Section 4.3, when a multi-component subscript is specified
(y = x[i,j]), Python automatically stores the components in a tuple in the order listed within the brackets and passes the tuple to the ndxTuple argument.
The contents of the ndxTuple are passed to the _computeIndex helper method to compute the index offset within the 1-D storage array. The use of the helper method reduces the need for duplicate code that otherwise would be required in both element access methods. Here is the definition of the __getitem__ method:
def __getitem__(self, ndxTuple) :
assert len(ndxTuple) == self.numDims(), "Invalid # of array subscripts."
index = self._computeIndex(ndxTuple)
assert index is not None, "Array subscript out of range."
return self._elements[index]
The __setitem__ operator method can be implemented in a similar fashion. The major difference is that this method requires a second argument to receive the value to which an element is set and modifies the indicated element with the new value instead of returning a value:
def __setitem__(self, ndxTuple, value) :
assert len(ndxTuple) == self.numDims(), "Invalid # of array subscripts."
index = self._computeIndex(ndxTuple)
assert index is not None, "Array subscript out of range."
self._elements[index] = value
Clearing the elements of the array to a specific value is as simple as calling the clear method on the _elements array, the 1-D storage array:
def clear(self, value) :
self._elements.clear(value)
Computing the Offset
The _computeIndex helper method implements equation X, which computes the offset within the 1-D storage array.
def _computeIndex(self, idx) :
offset = 0
for j in range(len(idx)) :
if idx[j] < 0 or idx[j] >= self._dims[j] :
return None
else :
offset += idx[j] * self._factors[j]
return offset
The method must also verify the subscript components are within the legal range of the dimension lengths. If they are valid, the offset is computed and returned; otherwise, None is returned to flag an invalid array index. By returning None from the helper method instead of raising an exception within the method, better information can be provided to the programmer as to the exact element access operation that caused the error. The implementation of the Multiarray class is provided below
Program Listing
# Implementation of the MultiArray ADT using a 1-D array. class MultiArray : # Creates a multi-dimensional array. def __init__(self, *dimensions) : assert len(dimensions) > 1, "The array must have 2 or more dimensions." # The variable argument tuple contains the dim sizes. self._dims = dimensions # Compute the total number of elements in the array. size = 1 for d in dimensions : assert d > 0, "Dimensions must be > 0." size *= d # Create the 1-D array to store the elements. self._elements = Array(size) # Create a 1-D array to store the equation factors. self._factors = Array(len(dimensions)) self._computeFactors() # Returns the number of dimensions in the array. def numDims(self) : return len(self._dims) # Returns the length of the given dimension. def length(self, dim) : assert dim >= 1 and dim < len(self._dims),\ "Dimension component out of range." return self._dims[dim - 1] # Clears the array by setting all elements to the given value. def clear(self, value) : self._elements.clear(value) # Returns the contents of element (i_1, i_2, ..., i_n). def __getitem__(self, ndxTuple) : assert len(ndxTuple) == self.numDims(), "Invalid # of array subscripts." index = self._computeIndex(ndxTuple) assert index is not None, "Array subscript out of range." return self._elements[index] # Sets the contents of element (i_1, i_2, ..., i_n). def __setitem__(self, ndxTuple, value) : assert len(ndxTuple) == self.numDims(), "Invalid # of array subscripts." index = self._computeIndex(ndxTuple) assert index is not None, "Array subscript out of range." self._elements[index] = value # Computes the 1-D array offset for element (i_1, i_2, ... i_n) # using the equation i_1 * f_1 + i_2 * f_2 + ... + i_n * f_n def _computeIndex(self, idx) : offset = 0 for j in range(len(idx)) : # Make sure the index components are within the legal range. if idx[j] < 0 or idx[j] >= self._dims[j] : return None else : # sum the product of i_j * f_j. offset += idx[j] * self._factors[j] return offset # Computes the factor values used in the index equation. def _computeFactors( self ): ......
|