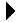To determine the efficiency of an algorithm, we can examine the solution itself and measure those aspects of the algorithm that most critically affect its execution time. For example, we can count the number of logical comparisons, data interchanges, or arithmetic operations. Consider the following algorithm for computing the sum of each row of an matrix and an overall sum of the entire matrix:
totalSum = 0 # Version 1
for i in range(n) :
rowSum[i] = 0
for j in range(n) :
rowSum[i] = rowSum[i] + matrix[i,j]
totalSum = totalSum + matrix[i,j]
Suppose we want to analyze the algorithm based on the number of additions performed. In this example, there are only two addition operations, making this a simple task. The algorithm contains two loops, one nested inside the other. The inner loop is executed times and since it contains the two addition operations, there are a total of additions performed by the inner loop for each iteration of the outer loop. The outer loop is also performed times, for a total of additions.
Can we improve upon this algorithm to reduce the total number of addition operations performed? Consider a new version of the algorithm in which the second addition is moved out of the inner loop and modified to sum the entries in the rowSum array instead of individual elements of the matrix.
totalSum = 0 # Version 2
for i in range(n) :
rowSum[i] = 0
for j in range(n) :
rowSum[i] = rowSum[i] + matrix[i,j]
totalSum = totalSum + rowSum[i]
In this version, the inner loop is again executed $n$ times, but this time, it only contains one addition operation. That gives a total of additions for each iteration of the outer loop, but the outer loop now contains an addition operator of its own. To calculate the total number of additions for this version, we take the additions performed by the inner loop and add one for the addition performed at the bottom of the outer loop. This gives additions for each iteration of the outer loop, which is performed times for a total of additions.
If we compare the two results, it's obvious the number of additions in the second version is less than the first for any greater than 1. Thus, the second version will execute faster than the first, but the difference in execution times will not be significant. The reason is that both algorithms execute on the same order of magnitude, namely . Thus, as the size of increases, both algorithms increase at approximately the same rate (though one is slightly better), as illustrated numerically in Table 5.1.1 and graphically in Figure 5.1.1.
| n | 2n2 | n2 + n |
|---|
| 10 |
200 |
110 |
| 100 |
20,000 |
10,100 |
| 1000 |
2,000,000 |
1,001,000 |
| 10000 |
200,000,000 |
100,010,000 |
| 100000 |
20,000,000,000 |
10,000,100,000 |
Table 5.1.1: Growth rate comparisons for different input sizes.
Figure 5.1.1: Graphical comparison of the growth rates from Table 5.1.1