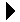6.5 The Bubble Sort

A simple solution to the sorting problem is the bubble sort algorithm, which re-arranges the values by iterating over the sequence multiple times, causing larger values to bubble to the top or end of the list. To illustrate how the bubble sort algorithm works, suppose we have four playing cards that we want to order from smallest to largest face value. We start by laying the cards out face up on a table as shown here:

The algorithm requires multiple passes over the cards, with each pass starting at the first card and ending one card earlier than on the previous iteration. During each pass, the cards in the first and second positions are compared. If the first is larger than the second, the two cards are swapped.

Next, the cards in positions two and three are compared. If the first one is larger than the second, they are swapped. Otherwise, we leave them as they were.

This process continues for each successive pair of cards until the card with the largest face value is positioned at the end.

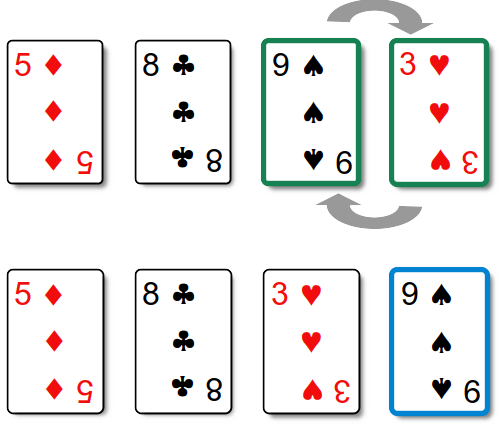
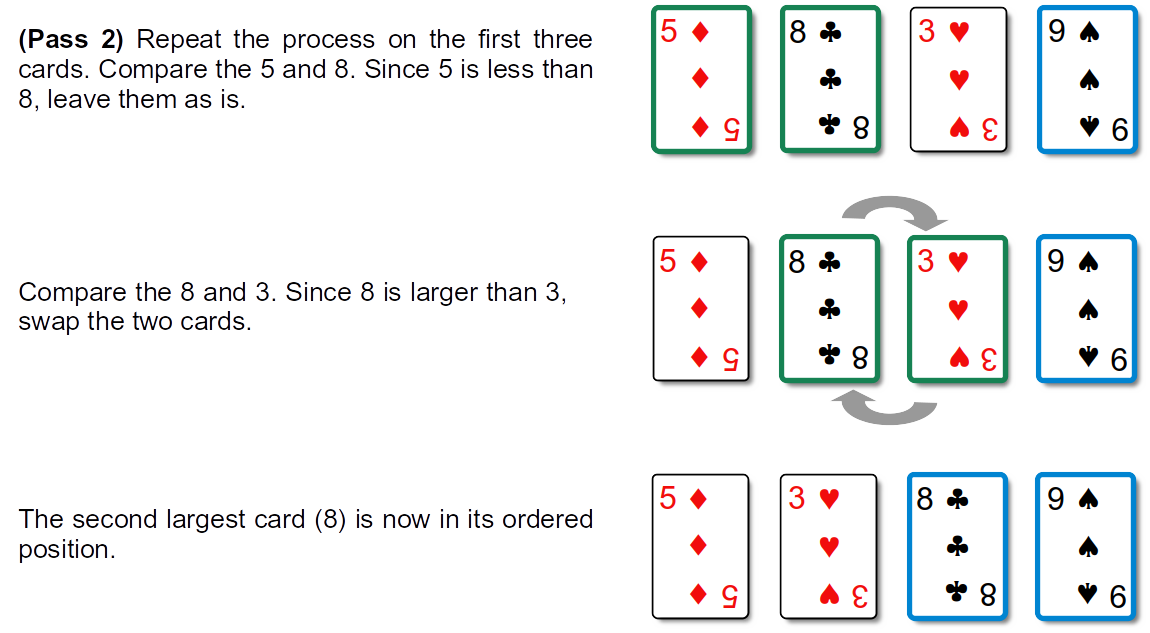
The next two passes over the cards are illustrated below. In the second pass the card with the second largest face value is positioned in the next-to-last position.

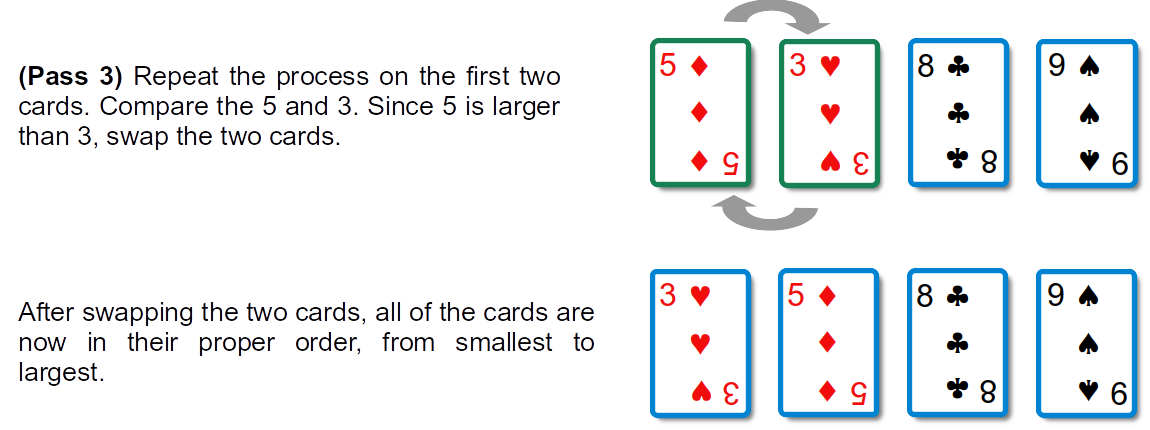
In the third and final pass, the first two cards will be positioned correctly.

Implementation

A Python implementation of the bubble sort algorithm is provided below.

Figure 6.5.1 illustrates the swaps performed during the first pass of the algorithm when applied to an array containing 11 integer values.

Figure 6.5.1: First complete pass of the bubble sort algorithm that places 64 in its correct position. Black boxes represent values being compared; arrows indicate exchanges.

Figure 6.5.2 shows the ordering of the values within the array after each iteration of the outer loop.

Figure 6.5.2: Result of applying the bubble sort algorithm to the sample sequence. The gray boxes show the values that are in order after each outer-loop traversal.

Efficiency

The efficiency of the bubble sort algorithm only depends on the number of keys in the array and is independent of the specific values and the initial arrangement of those values. To determine the efficiency, we must determine the total number of iterations performed by the inner loop for a sequence containing $n$ values. The outer loop is executed $n-1$ times since the algorithm makes $n-1$ passes over the sequence. The number of iterations for the inner loop is not fixed, but depends on the current iteration of the outer loop. On the first pass over the sequence, the inner loop executes $n-1$ times; on the second pass, $n-2$ times; on the third, $n-3$ times, and so on until it executes once on the last pass. The total number of iterations for the inner loop will be the sum of the first $n-1$ integers, which equals

$$\frac{n(n-1)}{2}-n=\frac{1}{2}{n}^2+\frac{1}{2}n$$

bubble sort

worst-case: $\text{O}\left(n^2\right)$

resulting in a run time of $\text{O}\left(n^2\right)$. Bubble sort is considered one of the most inefficient sorting algorithms due to the total number of swaps required. Given an array of keys in reverse order, a swap is performed for every iteration of the inner loop, which can be costly in practice.

The bubble sort algorithm as implemented above always performs $n^2$ iterations of the inner loop. But what if the sequence is already in sorted order? In this case, there would be no need to sort the sequence. But our implementation still performs all $n^2$ iterations because it has no way of knowing the sequence is already sorted.

The bubble sort algorithm can be improved by having it terminate early and not require it to perform all $n^2$ iterations when the sequence is in sorted order. We can determine the sequence is in sorted order when no swaps are performed by the if statement within the inner loop. At that point, the function can return immediately without completing the remaining iterations. If a value is out of sorted order, then it will either be smaller than its predecessor in the sequence or larger than its successor at which point the condition of the if statement would be true. This improvement, which is left as an exercise, introduces a best case that only requires $\text{O}\left(n\right)$ time when the initial input sequence is in sorted order.