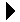6.6 The Selection Sort

A second sorting algorithm, which improves on the bubble sort and works in a fashion similar to what a human may use to sort a list of values, is known as the selection sort. We can again use the set of playing cards to illustrate the algorithm and start by placing five cards face up on a table that are to be sorted in ascending order.

Instead of swapping the cards as was done with the bubble sort, we are going to scan through the cards and select the smallest from among those on the table and place it in our hand. For our set of cards, we identify the 3 as the smallest:

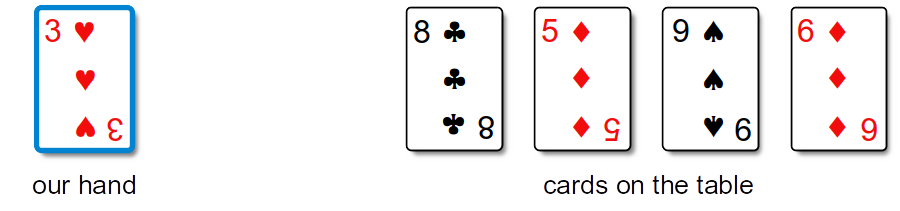
We pick up the 3 and place it in our hand, leaving the remaining cards on the table:

We repeat the process and identify the 5 as the next smallest face value:

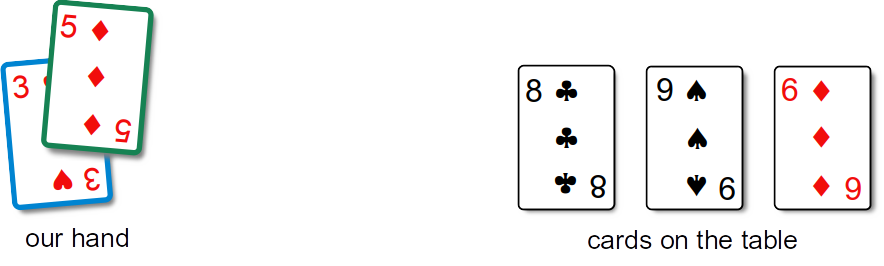
We pick up the 5 and add it to proper sorted position, which will be on the right side since there are no cards with a smaller face value left on the table.

This process is continued until all of the cards have been picked up and placed in our hand in the correct sorted order from smallest to largest.

The process we used to sort the set of five cards is similar to the approach used by the selection sort algorithm. But when implementing insertion sort in code, the algorithm maintains both the sorted and unsorted values within the same sequence structure. The selection sort, which improves on the bubble sort, makes multiple passes over the sequence, but unlike the bubble sort, it only makes a single swap after each pass. The implementation of the selection sort algorithm is provided below.

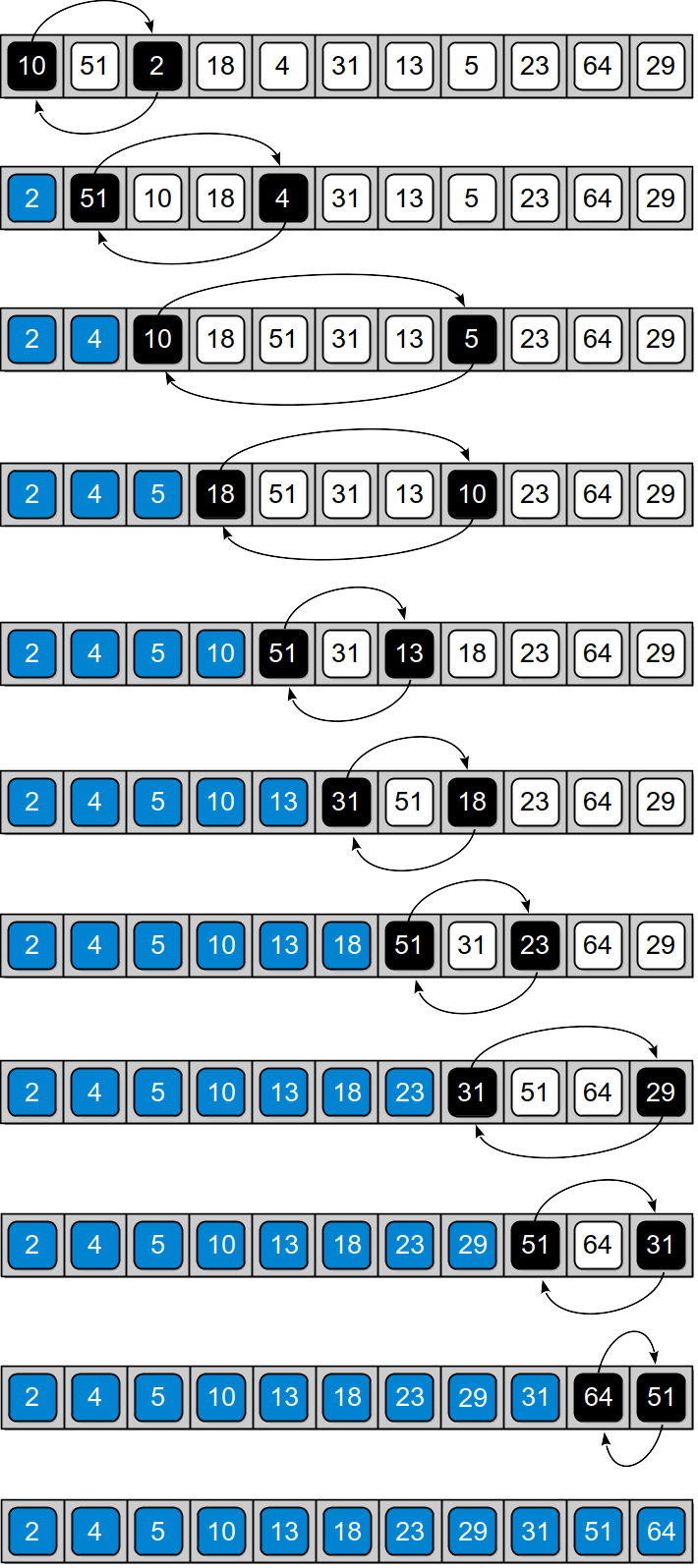
The process starts by finding the smallest value in the sequence and swaps it with the value in the first position of the sequence. The second smallest value is then found and swapped with the value in the second position. This process continues positioning each successive value by selecting them from those not yet sorted and swapping with the values in the respective positions. Figure 6.6.1 shows the results after each iteration of the algorithm when applied to the sample array of integers. The blue boxes represent those items already placed in their proper position while the black boxes show the two values that are swapped.

Figure 6.6.1: Result of applying the selection sort algorithm to our sample array. The blue boxes show the values that have been sorted; the black boxes show the values that are swapped during each iteration of the algorithm.

selection
sort

worst-case: $\text{O}\left(n^2\right)$

The selection sort, which makes $n-1$ passes over the array to reposition $n-1$ values, is also $\text{O}\left(n^2\right)$. The difference between the selection and bubble sorts is that the selection sort reduces the number of swaps required to sort the list to $\text{O}\left(n\right)$.