6.7 The Insertion Sort

Another commonly studied sorting algorithm is the insertion sort. Continuing with our analogy of sorting a set of playing cards to illustrate the sorting algorithms, consider five cards stacked in a deck face up:

We pick up the top card from the deck and place it in our hand:

Since this is the first card, there is no decision to be made as to its position. We again pick up the top card from the deck and compare it to the card already in our hand and insert it into its proper sorted position:

After placing the 8 into our hand, the process is repeated. This time, we pick up the 5 and find its position within our hand and insert it in the proper place:

This process continues, one card at a time, until all of the cards have been removed from the table and placed into our hand in their proper sorted position.

The insertion sort maintains a collection of sorted items and a collection of items to be sorted. In the playing card analogy, the deck represents the collection to be sorted and the cards in our hand represents those already sorted. When implementing insertion sort in a program, the algorithm maintains both the sorted and unsorted collections within the same sequence structure. The algorithm keeps the list of sorted values at the front of the sequence and picks the next unsorted value from the first of those yet to be positioned. To position the next item, the correct spot within the sequence of sorted values is found by performing a search. After finding the proper position, the slot has to be opened by shifting the items down one position. A Python implementation of the insertion sort algorithm is provided below.

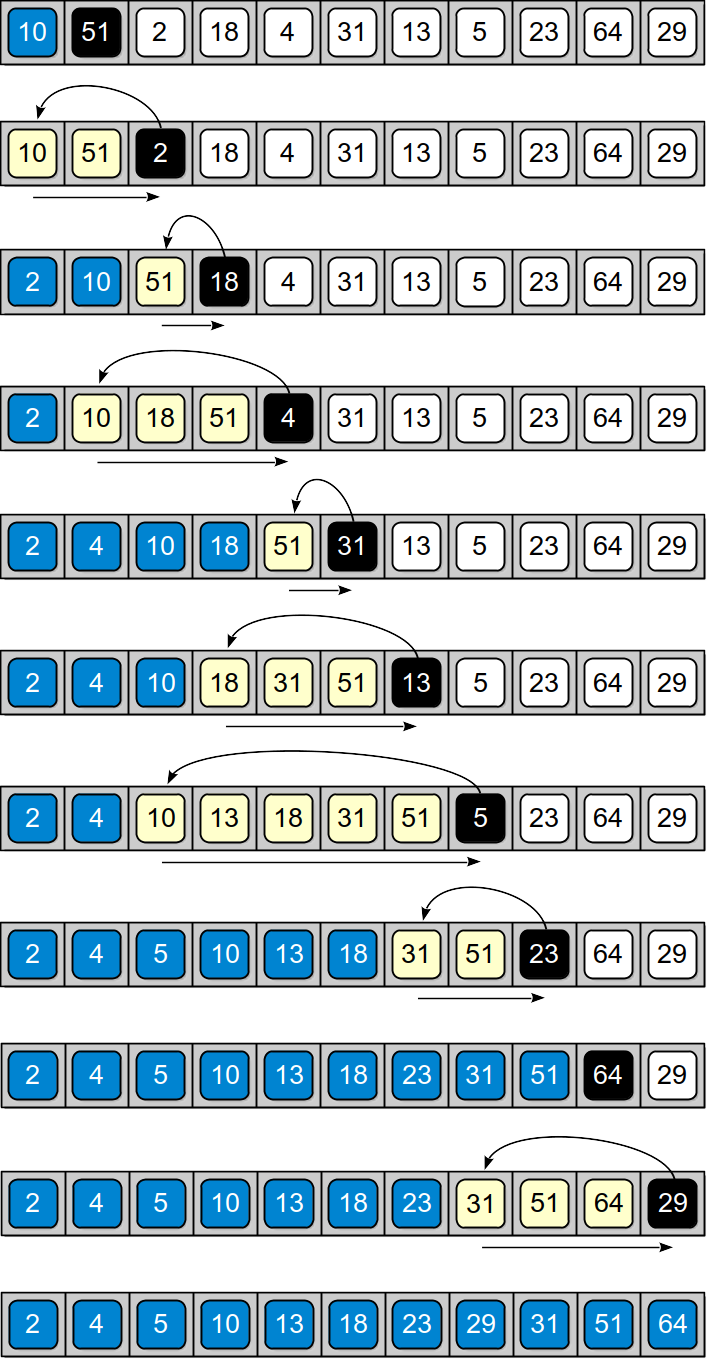
The insertionSort function starts by assuming the first item is in its proper position. Next, an iteration is performed over the remaining items so each value can be inserted into its proper position within the sorted portion of the sequence. The ordered portion of the sequence is at the front while those yet to be inserted are at the end. The i loop index variable marks the separation point between the two parts. The inner loop is used to find the insertion point within the sorted sequence and at the same time, shifts the items down to make room for the next item. Thus, the inner loop starts from the end of the sorted subsequence and works its way to the front. After finding the proper position, the item is inserted. Figure 6.7.1 illustrates the application of this algorithm on an array of integer values.

The insertion sort is an example of a sorting algorithm in which the best and worst cases are different. Determining the different cases and the corresponding run times is left as an exercise.

Figure 6.7.1: Result of applying the insertion sort algorithm to the sample array. The blue boxes show values that have been sorted; the black boxes show the next value to be positioned; and the yellow boxes are the sorted values that have to be shifted to the right to open a spot for the next value.