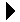8.4 Priority Queues

Some applications require the use of a queue in which items are assigned a priority and the items with a higher priority are dequeued first. However, all items with the same priority still obey the FIFO principle. That is, if two items with the same priority are enqueued, the first in will be the first out.

The Priority Queue ADT

A priority queue is simply an extended version of the basic queue with the exception that a priority $p$ must be assigned to each item at the time it is enqueued. There are two basic types of priority queues: bounded and unbounded. The bounded priority queue assumes a small limited range of $p$ priorities over the interval of integers $[0 \dots p)$ . The unbounded priority queue places no limit on the range of integer values that can be used as priorities. The definition of the Priority Queue ADT is provided below. Note that we use one definition for both bounded and unbounded priority queues, but with two different constructors.

The Priority Queue ADT

A priority queue is a queue in which each item is assigned a priority and items with a higher priority are removed before those with a lower priority, irrespective of when they were added. Integer values are used for the priorities with a smaller integer value having a higher priority. A bounded priority queue restricts the priorities to the integer values between zero and a predefined upper limit whereas an unbounded priority queue places no limits on the range of priorities.

PriorityQueue()

Creates a new empty unbounded priority queue.
BPriorityQueue()

Creates a new empty bounded priority queue with priority levels in the range from 0 to numLevels-1.
isEmpty()

Returns a Boolean value indicating whether the queue is empty.
length()

Returns the number of items currently in the queue.
enqueue(item, priority)

Adds the given item to the queue by inserting it in the proper position based on the given priority. The priority value must be within the legal range when using a bounded priority queue.
dequeue()

Removes and returns the front item from the queue, which is the item with the highest priority. The associated priority value is discarded. If two items have the same priority, then those items are removed in a FIFO order. An item cannot be dequeued from an empty queue.

Example Use

Consider the following code segment, which enqueues a number of items into a priority queue:

Q = PriorityQueue()

Q.enqueue("purple", 5)

Q.enqueue("black", 1)

Q.enqueue("orange", 3)

Q.enqueue("white", 0)

Q.enqueue("green", 1)

Q.enqueue("yellow", 5)

The abstract view of the resulting queue is shown in Figure 8.4.1.

Figure 8.4.1: Abstract view of a priority queue resulting from enqueuing several strings, along with individual priorities.

The first item to be removed will be the first item with the highest priority. Notice when items "black" and "green" are enqueued, "green" follows "black" in the queue even though they have the same priority since items with equal priority still obey the FIFO principle.

To illustrate the use of the priority queue, the following code segment removes the items and prints them to the terminal:

while not Q.isEmpty() :

  item = Q.dequeue()

  print(item)

which results in the following output:

white
black
green
orange
purple
yellow

8.3 Circular Array Implementation

Chapter 8. Queues

8.5 Unbounded Priority Queue