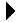6.3 Binary Search

The linear search algorithm for a sorted sequence produced a slight improvement over the linear search with an unsorted sequence, but both have a linear time-complexity in the worst case. To improve the search time for a sorted sequence, we can modify the search technique itself.

Consider an example where you are given a stack of exams, which are in alphabetical order, and are asked to find the exam for "Jessica Roberts." In performing this task, most people would not begin with the first exam and flip through one at a time until the requested exam is found, as would be done with a linear search. Instead, you would probably flip to the middle and determine if the requested exam comes alphabetically before or after that one. Assuming Jessica's paper follows alphabetically after the middle one, you know it cannot possibly be in the top half of the stack. Instead, you would probably continue searching in a similar fashion by splitting the remaining stack of exams in half to determine which portion contains Jessica's exam. This is an example of a divide and conquer strategy, which entails dividing a larger problem into smaller parts and conquering the smaller part.

Algorithm Description

The binary search algorithm works in a similar fashion to the process described above and can be applied to a sorted sequence. The algorithm starts by examining the middle item of the sorted sequence, resulting in one of three possible conditions: the middle item is the target value, the target value is less than the middle item, or the target is larger than the middle item. Since the sequence is ordered, we can eliminate half the values in the list when the target value is not found at the middle position.

Consider the task of searching for value 10 in the sorted array from Figure 6.2.2. We first determine which element contains the middle entry. As illustrated in Figure 6.3.1, the middle entry contains 18, which is greater than our target of 10. Thus, we can discard the upper half of the array from consideration since 10 cannot possibly be in that part. Having eliminated the upper half, we repeat the process on the lower half of the array. We then find the middle item of the lower half and compare its value to the target. Since that entry, which contains 5, is less than the target, we can eliminate the lower fourth of the array. The process is repeated on the remaining items. Upon finding value 10 in the middle entry from among those remaining, the process terminates successfully. If we had not found the target, the process would continue until either the target value was found or we had eliminated all values from consideration.

Figure 6.3.1: Searching for 10 in a sorted array using the binary search.

Question 6.3.1

Consider the sorted sequence below

Which elements of the sequence will be examined by the binary search algorithm, when searching for value 81?

To answer this question, click the "Start" button below and then drag the correct values from the right to the far left grid line and list them in the proper order in which the values are visited from first to last.

.29
.59
.81
-5
-16
-17
-23
-25
-36
-48
-64
-97

Implementation

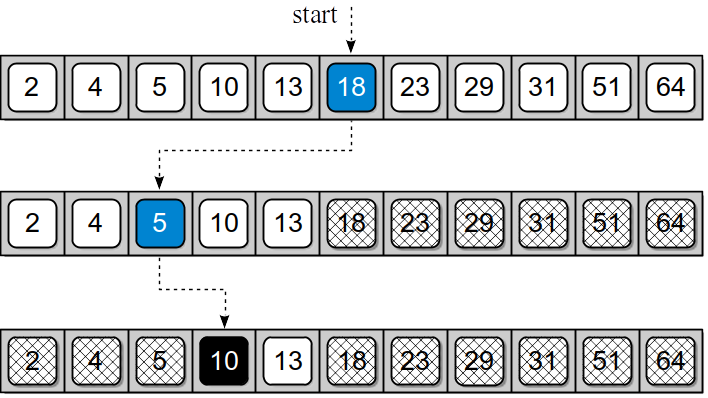
The binary search algorithm is implemented in the source listing below. The variables low and high are used to mark the range of elements in the sequence currently under consideration. When the search begins, this range is the entire sequence since the target item can be anywhere within the sequence. The first step in each iteration is to determine the midpoint of the sequence. If the sequence contains an even number of elements, the mid point will be chosen such that the left sequence contains one less item than the right. Figure 6.3.2 illustrates the positioning of the low, high, and mid markers as the algorithm progresses.

After computing the midpoint, the corresponding element in that position is examined. If the midpoint contains the target, we immediately return True. Otherwise, we determine if the target is less than the item at the midpoint or greater. If it is less, we adjust the high marker to be one less than the midpoint and if it is greater, we adjust the low marker to be one greater than the midpoint. In the next iteration of the loop, the only portion of the sequence considered are those elements between the low and high markers, as adjusted. This process is repeated until the item is found or the low marker becomes greater than the high marker. This condition occurs when there are no items left to be processed, indicating the target is not in the sorted sequence.

Figure 6.3.2: The steps performed by the binary search algorithm in searching for 10: (a) initial range of items, (b) locating the midpoint, (c) eliminating the upper half, (d) midpoint of the lower half, (e) eliminating the lower fourth, and (f) finding the target.

Run Time Analysis

binary search

worst-case: $\text{O}\left(\text{log}n\right)$

To evaluate the efficiency of the the binary search algorithm, assume the sorted sequence contains $n$ items. We need to determine the maximum number of times the while loop is executed. The worst case occurs when the target value is not in the sequence, the same as for the linear search. The difference with the binary search is that not every item in the sequence has to be examined before determining the target is not in the sequence, even in the worst case. Since the sequence is sorted, each iteration of the loop can eliminate from consideration half of the remaining values. As we saw earlier in Section 5.3, when the input size is repeatedly reduced by half during each iteration of a loop, there will be $\text{log}n$ iterations in the worst case. Thus, the binary search algorithm has a worst case time-complexity of $\text{O}\left(\text{log}n\right)$, which is more efficient than the linear search.

Question 6.3.2

The binary search algorithm can only be used with a sorted sequence. Briefly explain why it can not be used with an unsorted sequence.

Each iteration of the algorithm virtually splits the list in half based on the relationship of the target to the middle element and eliminates one half from further consideration. In an unsorted sequence, a value can appear anywhere within the sequence. Thus, when the unsorted sequence is split, the target value could actually be in the discarded half of the sequence, since none of the elements in the sequence have a specific relationship to the middle element.