We can design and implement a discrete event computer simulation to analyze the average time passengers have to wait for service at an airport ticket counter. The simulation will involve multiple ticket agents serving customers who have to wait in line until they can be served. Our design will be an object-oriented solution with multiple classes.
System Parameters
The program will prompt the user for the queuing system parameters:
Number of minutes to simulate: 25
Number of ticket agents: 2
Average service time per passenger: 3
Average time between passenger arrival: 2
For simplicity we use minutes as the discrete time units. This would not be sufficient to simulate a real ticket counter as multiple passengers are likely to arrive within any given minute. The program will then perform the simulation and produce the following output:
Number of passengers served = 12
Number of passengers remaining in line = 1
The average wait time was 1.17 minutes.
We will also have the program display event information, which can be used to help debug the program. The debug information lists each event that occurs in the system along with the time the events occur. For the input values shown above, the event information displayed will be:
Time 2: Passenger 1 arrived.
Time 2: Agent 1 started serving passenger 1.
Time 3: Passenger 2 arrived.
Time 3: Agent 2 started serving passenger 2.
Time 5: Passenger 3 arrived.
Time 5: Agent 1 stopped serving passenger 1.
Time 6: Agent 1 started serving passenger 3.
Time 6: Agent 2 stopped serving passenger 2.
Time 8: Passenger 4 arrived.
Time 8: Agent 2 started serving passenger 4.
Time 9: Agent 1 stopped serving passenger 3.
Time 10: Passenger 5 arrived.
Time 10: Agent 1 started serving passenger 5.
Time 11: Passenger 6 arrived.
Time 11: Agent 2 stopped serving passenger 4.
Time 12: Agent 2 started serving passenger 6.
Time 13: Passenger 7 arrived.
Time 13: Agent 1 stopped serving passenger 5.
Time 14: Passenger 8 arrived.
Time 14: Agent 1 started serving passenger 7.
Time 15: Passenger 9 arrived.
Time 15: Agent 2 stopped serving passenger 6.
Time 16: Agent 2 started serving passenger 8.
Time 17: Agent 1 stopped serving passenger 7.
Time 18: Passenger 10 arrived.
Time 18: Agent 1 started serving passenger 9.
Time 19: Passenger 11 arrived.
Time 19: Agent 2 stopped serving passenger 8.
Time 20: Agent 2 started serving passenger 10.
Time 21: Agent 1 stopped serving passenger 9.
Time 22: Agent 1 started serving passenger 11.
Time 23: Passenger 12 arrived.
Time 23: Agent 2 stopped serving passenger 10.
Time 24: Agent 2 started serving passenger 12.
Time 25: Passenger 13 arrived.
Time 25: Agent 1 stopped serving passenger 11.
Passenger Class
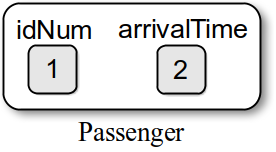
First, we need a class to store information related to a single passenger. We create a Passenger class for this purpose. The class will contain two data fields. The first is an identification number used in the output of the event information. The second field records the time the passenger arrives. This value will be needed to determine the length of time the passenger waited in line before beginning service with an agent. Methods are also provided to access the two data fields. An instance of the class is illustrated in Figure 8.8.1.
Figure 8.8.1: Sample Passenger object.
The complete implementation of this class is provided in the source listing below.
Program Listing
# Used to store and manage information related to an airline passenger. class Passenger : # Creates a passenger object. def __init__(self, idNum, arrivalTime) : self._idNum = idNum self._arrivalTime = arrivalTime # Gets the passenger's id number. def idNum(self) : return self._idNum # Gets the passenger's arrival time. def timeArrived(self) : return self._arrivalTime
|
Ticket Agent Class
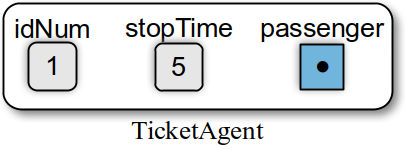
We also need a class to represent and store information related to the ticket agents. The information includes an agent identification number and a timer to know when the transaction will be completed. This value is the sum of the current time and the average time of the transaction as entered by the user. Finally, we need to keep track of the current passenger being served by the agent in order to identify the specific passenger when the transaction is completed. An instance of the class is shown in Figure 8.8.2
Figure 8.8.2: Sample TicketAgent object.
and the TicketAgent class is implemented in the listing below.
Program Listing
# Used to store and manage information related to an airline ticket agent. class TicketAgent : # Creates a ticket agent object. def __init__(self, idNum) : self._idNum = idNum self._passenger = None self._stopTime = -1 # Gets the ticket agent's id number. def idNum(self) : return self._idNum # Determines if the ticket agent is free to assist a passenger. def isFree(self) : return self._passenger is None # Determines if the ticket agent has finished helping the passenger. def isFinished(self, curTime) : return self._passenger is not None and self._stopTime == curTime # Indicates the ticket agent has begun assisting a passenger. def startService(self, passenger, stopTime) : self._passenger = passenger self._stopTime = stopTime # Indicates the ticket agent has finished helping the passenger. def stopService(self) : thePassenger = self._passenger self._passenger = None return thePassenger
|
The _passenger field is set to a null reference, which will be used to flag a free agent. The idNum method simply returns the id assigned to the agent when the object is created while the isFree method examines the _passenger field to determine if the agent is free. The isFinished method is used to determine if the passenger currently being served by this agent has completed her transaction. This method only flags the transaction as having been completed. To actually end the transaction, stopService must be called. stopService sets
the _passenger field to None to again indicate the agent is free and returns the passenger object. To begin a transaction, startService is called, which assigns the appropriate fields with the supplied arguments.
Simulation Class
Finally, we construct the TicketCounterSimulation class to manage the actual simulation. This class will contain the various components, methods, and data values required to perform a discrete event simulation. A sample instance is
illustrated in Figure 8.8.3.
Figure 8.8.3: A sample TicketCounterSimulation object.
The first step in the constructor is to initialize three simulation parameters. Note the _arriveProb is the probability of a passenger arriving during the current time step using the formula described earlier. A queue is created, which will be used to represent the line in which passengers must wait until they are served by a ticket agent. The ticket agents are represented as an array of \class{Agent} objects. The individual objects are instantiated and each is assigned an id number, starting with 1. Two data fields are needed to store data collected during the actual simulation. The first is the summation of the time each passenger has to wait in line before being served, and the second keeps track of the number of passengers in the simulation. The latter will also be used to assign an id to each passenger.
The simulation is performed by calling the run method, which simulates the ticking of the clock by performing a count-controlled loop keeping track of~the current time in curTime. The loop executes until numMinutes have elapsed. The events of the simulation are also performed during the terminating minute, hence, the need for the _numMinutes + 1 in the range function. During each
iteration of the loop, the three simulation rules outlined earlier are handled by the respective _handleXYZ helper methods. The _handleArrival method determines if a passenger arrives during the current time step and handles that arrival. _handleBeginService determines if any agents are free and allows
the next passenger(s) in line to begin their transaction. The _handleEndService determines which of the current transactions have completed, if any, and flags a passenger departure. A partial implemenation of the Simulation class is provided below. The implementation of the helper methods is left as an exercise.
Program Listing
# Implementation of the main simulation class. from ezarrays import Array from llistqueue import Queue from simpeople import TicketAgent, Passenger class TicketCounterSimulation : # Create a simulation object. def __init__(self, numAgents, numMinutes, betweenTime, serviceTime) : # Parameters supplied by the user. self._arriveProb = 1.0 / betweenTime self._serviceTime = serviceTime self._numMinutes = numMinutes # Simulation components. self._passengerQ = Queue() self._theAgents = Array( numAgents ) for i in range( numAgents ) : self._theAgents[i] = TicketAgent(i+1) # Computed during the simulation. self._totalWaitTime = 0 self._numPassengers = 0 # Run the simulation using the parameters supplied earlier. def run(self) : for curTime in range(self._numMinutes + 1) : self._handleArrival( curTime ) self._handleBeginService( curTime ) self._handleEndService( curTime ) # Print the simulation results. def printResults(self) : numServed = self._numPassengers - len(self._passengerQ) avgWait = float( self._totalWaitTime ) / numServed print("") print("Number of passengers served = ", numServed) print("Number of passengers remaining in line = %d" % len(self._passengerQ)) print("The average wait time was %4.2f minutes." % avgWait) # The remaining methods that have yet to be implemented. # def _handleArrive( curTime ): # Handles simulation rule #1. # def _handleBeginService( curTime ): # Handles simulation rule #2. # def _handleEndService( curTime ): # Handles simulation rule #3.
|
After running the simulation, the printResults method is called to print the results. When the simulation terminates there may be some passengers remaining in the queue who have not yet been assisted. Thus, we need to determine how many passengers have exited the queue, which indicates the number of passenger wait times included in the _totalWaitTime field. The average wait time is simply the total wait time divided by the number of passengers served.
The last component of our program is the driver module, which is left as an exercise. The driver extracts the simulation parameters from the user and then creates and uses a TicketCounterSimulation object to perform the simulation. To produce the same results shown earlier, you will need to seed the random number generator with the value 4500 before running the simulation:
In a typical experiment, a simulation is performed multiple times varying the parameters with each execution. Table 8.8.1 illustrates the results of a single experiment with multiple executions of the simulation. Note the significant change in the average wait time when increasing the number of ticket agents by one in the last two sets of experiments.
Num
Minutes | Num
Agents | Average
Service | Time
Between | Average
Wait | Passengers
Served | Passengers
Remaining |
|---|
| 100 |
2 |
3 |
2 |
2.49 |
49 |
2 |
| 500 |
2 |
3 |
2 |
3.91 |
240 |
0 |
| 1000 |
2 |
3 |
2 |
10.93 |
490 |
14 |
| 5000 |
2 |
3 |
2 |
15.75 |
2459 |
6 |
| 10000 |
2 |
3 |
2 |
21.17 |
4930 |
18 |
|
|
| 100 |
2 |
4 |
2 |
10.60 |
40 |
11 |
| 500 |
2 |
4 |
2 |
49.99 |
200 |
40 |
| 1000 |
2 |
4 |
2 |
95.72 |
400 |
104 |
| 5000 |
2 |
4 |
2 |
475.91 |
2000 |
465 |
| 10000 |
2 |
4 |
2 |
949.61 |
4000 |
948 |
|
|
| 100 |
3 |
4 |
2 |
0.51 |
51 |
0 |
| 500 |
3 |
4 |
2 |
0.50 |
240 |
0 |
| 1000 |
3 |
4 |
2 |
1.06 |
501 |
3 |
| 5000 |
3 |
4 |
2 |
1.14 |
2465 |
0 |
| 10000 |
3 |
4 |
2 |
1.21 |
4948 |
0 |
Table 8.8.1: Sample results of the ticket counter simulation experiment.